Diketahui AC = AE dan m∠BAC = m∠DAE Tunjukkan Bahwa

Perhatikan gambar berikut. Pada gambar di atas, ABCD adal...

Pada gambar diatas diketahui ∠AQF = ∠DPE. Pasangan garis yang sejajar pada gambar itu adalah… Pembahasan. ∠AQF dan ∠DPE adalah sudut-sudut luar berseberangan. Karena kedua sudut tersebut sama besar maka garis AB dan CD adalah dua garis sejajar.

Persamaan Grafik Fungsi Kuadrat Pada Gambar Diatas Adalah retorika

Menentukan Panjang Garis Bagi pada Segitiga. Garis bagi sebuah segitiga adalah garis yang ditarik dari titik sudut segitiga memotong sisi didepan titik sudut tersebut dengan membagi dua sama besar suudut tersebut, seperti gambar berikut. Dalil-dalil yang berlaku pada garis bagi segitiga yaitu : 1).

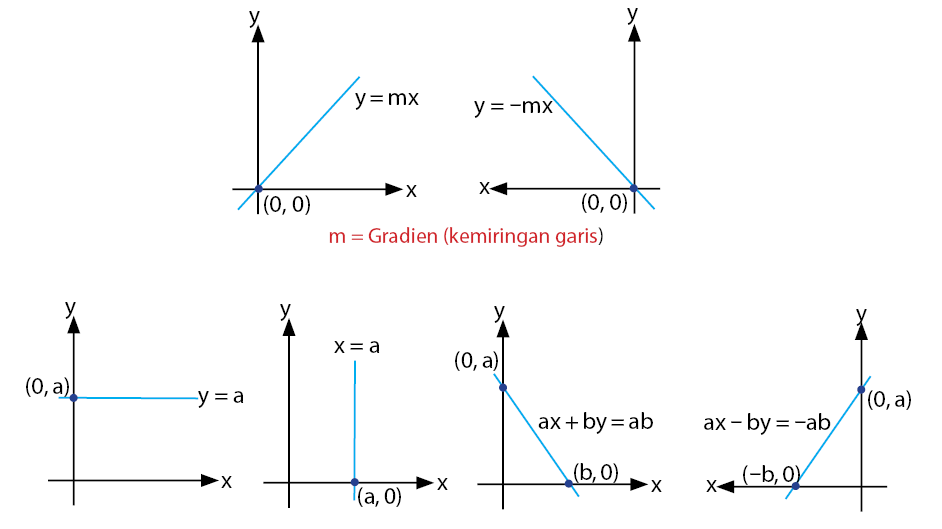
Persamaan Garis Lurus Pada Gambar Diatas Adalah IMAGESEE

Pembahasan Ingat definisi tangen sudut x berikut. tan x = sisi samping sisi depan Oleh karena itu, diperoleh: tan ∠ BAE = AB BE = 20 BE tan ∠ BAC = = = = = = tan ( ∠ BAE + ∠ EAC ) tan ( ∠ BAE + ∠ BAE ) tan ( 2 ⋅ ∠ BAE ) AB BC 20 20 1 Selanjutnya, ingat rumus tangen sudut rangkap berikut.

Pada Gambar Di Atas denah

Garis Bagi Suatu Segitiga. Garis Bagi adalah garis yang menghubungkan satu titik ke sisi di hadapannya dan menjadikannya dua sudut sama besar. Di gambar terlihat kalau garis AD membagi sudut BAC jadi 2 bagian sama besar, kan. Yaitu sudut BAD = sudut CAD. Oleh karena itu, garis AD disebut dengan garis bagi.

Pada gambar di atas, KP sejajar LR dan MP sejajar NR....

Ini penjelasan garis bagi, garis berat, dan garis tinggi pada segitiga.. terdapat garis-garis pada segitiga, yakni pada gambar berikut: garis-garis pada segitiga Keterangan: CF disebut garis tinggi;. CD = 10 cm, dan AE = 18 cm, maka panjang sisi BC adalah.. A. 20 cm B. 18 cm C. 16 cm D. 14 cm. Jawab: BC x AE = AB x CD BC x 18 = 36 x 10.

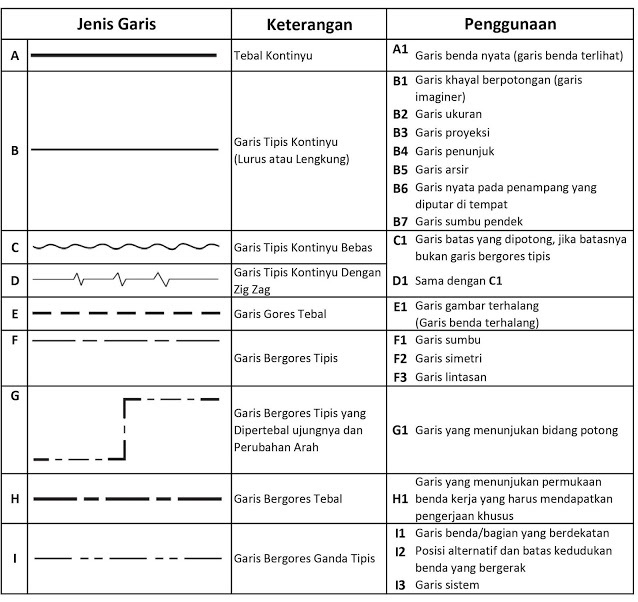
JenisJenis Garis pada Gambar Teknik Beserta Fungsinya Gerai Teknologi

1. Pada segitiga ABC sama kaki dengan puncak A, AD adalah garis tinggi dengan D pada sisi BC. Titik E adalah titik pada AC sehingga DE garis tinggi segitiga ADC. Jika dan , maka nilai dari adalah.. a. 4 b. 3 c. 2 d. 1 Solusi: Perhatikan dan sebangun , maka : 2.

Diketahui AC = AE dan m∠BAC = m∠DAE Tunjukkan Bahwa

Perhatikan gambar berikut ini: Garis Istimewa Pada Segitiga dan Rumus Cara Menghitungnya Google Image - Garis Istimewa Pada Segitiga dan Rumus Cara Menghitungnya Gambar diatas jelas bahwa garis putus - putus yang menghubungkan sudut C dengan garis AB adalah altitude atau garis tinggi. Garis ini merupakan garis bantu untuk mencari sisi AC.

pada gambar diatas diketahui besar Waktunya Belajar

Ada sebuah teorema dalam segitiga yang berbunyi kurang lebih sebagai berikut: Garis bagi membagi sisi di depannya menjadi dua bagian yang berbanding seperti sisi-sisi yang berdekatan. Untuk lebih jelasnya, coba perhatikan gambar di samping. Akan dibuktikan bahwa . Buktinya adalah sebagai berikut: Untuk berlatih, silakan lihat contoh soal yang.

Pada Gambar Di Samping Garis K Dan L Terbaru

Ada empat macam garis istimewa pada sebuah segitiga yaitu: • Garis bagi. • Garis tinggi. • Garis berat. • Garis sumbu. Pengertian Garis Bagi. Definisi garis bagi dalam sebuah segitiga adalah garis lurus yang menghubungkan satu titik sudut segitiga ke sisi dihadapannya dan membagi sudut tersebut menjadi dua sama besar.

Pada gambar diatas ini jika ∠ BAC = 60° maka panjang garis AB adalah... cma. 4b. 2√2c. 2√3d. 4√

Jenis-jenis segitiga berdasarkan besar sudutnya : 3). sudut refleks ( 180∘ < x < 360∘ 180 ∘ < x < 360 ∘ ). *). Segitiga lancip, gambar (a) Segitiga lancip adalah segitiga yang ketiga sudutnya merupakan sudut lancip, sehingga sudut-sudut yang terdapat pada segitiga tersebut besarnya antara 0∘ 0 ∘ dan 90∘ 90 ∘.

Pada gambar di atas, PL tegak lurus KM . Besar penyiku

1. Diketahui segi-tiga ABC, segmen garis AD adalah garis bagi sudut BAC. Mengapa titik pada garis AD letaknya sama jauh dari garis AC dan dari garis AB. Tunjukan. 2. Andai ada segi-tiga ABC. Andaikan garis AD adalah garis bagi dari sudut BAC. Andaikan garis BE adalah garis bagi dari sudut luar CBF dan garis CH adalah garis bagi dari

D C F E A B Pada gambar di atas, AE garis bagi BAC, dan E...

Ketiga garis bagi pada segitiga bertemu di satu titik. Titik inilah yang menjadi pusat lingkaran dalam. Apakah AE = EC ? Jawabannya belum tentu. Kesamaan AE = EC bisa terjadi kalau AB = BC. Atau jika AE = EC, maka garis BE adalah garis berat. Jadi kalau garis berat pasti membagi sisinya sama panjang.. Dari gambar diperoleh. CA = CE + AE. 26.

Garis Gradien Yang Tegak Lurus Ab Adalah

Apabila pada segitiga siku-siku diatas dibuat garis dari sudut A ke sisi miring BC maka akan diperoleh rumus: AB 2 = BD x BC AC 2 = CD x CB AD 2 = BD x CD. B. Kekongruenan. Kekongruenan dilambangkan dengan ≅. Kedua benda dikatakan kongruen jika memiliki bentuk dan ukuran yang sama. 1. Dua bangun datar yang kongruen

14+ Paling Baru Pada Gambar Di Atas Pasangan Garis Yang Sejajar Adalah

Jadi, kalau menuliskan garis sejajar pada gambar, bisa dengan AB // BC. 2. Garis Berpotongan. Garis berpotongan adalah garis yang terletak dalam satu bidang dan dapat bertemu di satu titik yang sama. Titik pertemuan itu disebut titik perpotongan. Contohnya adalah pada tanda silang "x". Ilustrasi garis berpotongan. (Arsip Zenius)

Luas Jajargenjang Abcd Pada Gambar Diatas Adalah Kondisko Rabat

a. Perhatikan gambar pada soal Diketahui AC = AE (sisi) Diketahui m ∠ BAC = m ∠ DAE (sudut) Perhatikan segitiga ABC dan ADE adalah segitiga siku-siku dimana m ∠ ABC = m ∠ ADE = 9 0 ∘ (sudut) Dari ketiga hal tersebut, terbukti ABC ≅ ADE karena memenuhi kriteria no 2 yaitu sisi-sudut-sudut. b.

14+ Paling Baru Pada Gambar Di Atas Pasangan Garis Yang Sejajar Adalah

Pembahasan Ingat! Kriteria dua segitiga kongruen adalah dua sudut yang bersesuaian sama besar dan sepasang sisi yang didepansalah satusudut itu sama panjang (sisi-sudut-sudut) Rumus Pythagoras sisi miring segitiga alas segitiga tinggi segitiga = = = alas segitiga 2 + tinggi segitiga 2 sisi miring segitiga 2 − tinggi segitiga 2 sisi miring segitiga 2 − alas segitiga 2 Perhatikan gambar berikut.