Menentukan Fungsi dari suatu grafik trigonometri YouTube

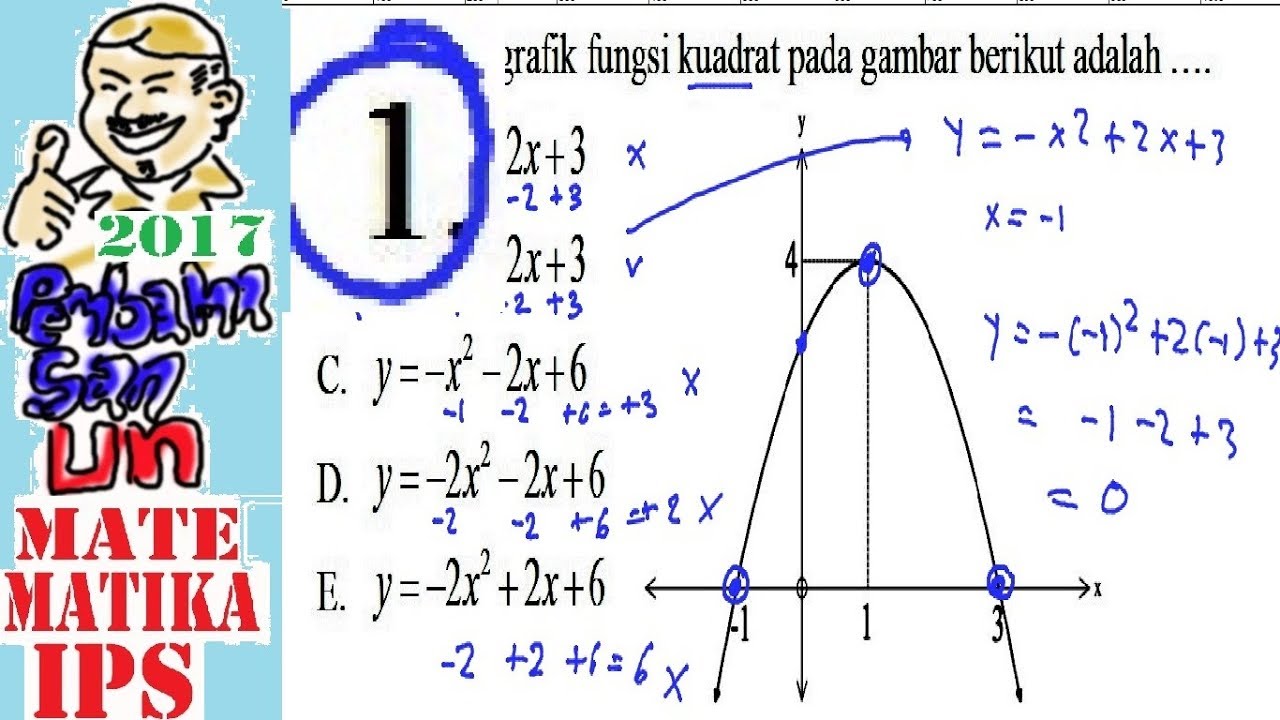
Cara Mencari Persamaan Grafik Fungsi Kuadrat Dari Gambar Matematika Dasar Riset

Karena keduanya berbeda, maka cara menentukannya juga berbeda, guys. Dari persamaan garis seperti ini, gradien akan mudah dicari, yaitu "m". Supaya lebih jelas, kamu bisa lihat contoh di bawah ini: Garis y = 2x + 3, maka gradien garis tersebut adalah 2. Garis y = -2x + 5, maka gradien garis tersebut adalah -2.

Contoh Soal Persamaan Grafik Fungsi Kuadrat Berbagai Contoh Riset

Contoh 2. Sketsakan grafik fungsi dengan terlebih dahulu menentukan asimtotnya! Pembahasan: Daerah asal dari fungsi adalah untuk setiap , sebab tidak ada nilai yang menyebabkan penyebutnya bernilai nol. Karena pangkat tertinggi pada pembilang, yakni lebih kecil dari pangkat tertinggi pada penyebut, yakni , maka asimtot datarnya adalah .

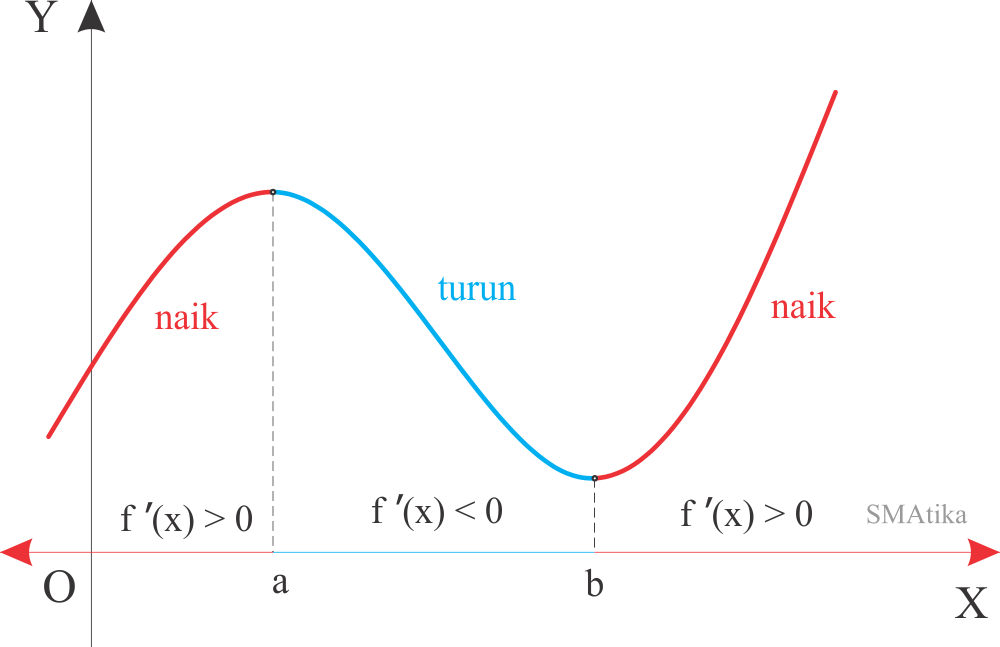
Menentukan Interval Fungsi Naik dan Fungsi Turun

Namanya adalah fungsi linear, yaitu fungsi yang pangkat tertingginya sama dengan satu makanya nama lain dari fungsi ini adalah polinom berderajat 1. Secara umum, rumus fungsi matematika jenis linear ini adalah sebagai berikut: f (x) = ax + b, dengan a≠0. Contoh: f (x) = x+3 → a=1, b=3. contoh fungsi linear.

Perbedaan Gambar Dan Grafik Fungsi Linear IMAGESEE

Ada tiga macam rumus yang bisa kita pakai untuk merumuskan fungsi kuadrat berdasarkan grafik, yaitu: 1. Jika pada grafik diketahui 2 titik sembarang pada sumbu x, maka menggunakan rumus y = a (x - x1) (x - x2) 2. Jika pada grafik diketahui titik puncak (xp, yp) dan 1 titik sembarang, maka menggunakan rumus y = a (x - xp)2 + yp.

Contoh Soal Persamaan Grafik Fungsi Kuadrat Dan Penyelesaiannya

F = G m1m2 r2 F = G m 1 m 2 r 2. Grafik Fungsi. Bilamana daerah asal dan daerah hasil sebuah fungsi merupakan bilangan riil, kita dapat membayangkan fungsi itu dengan menggambarkan grafiknya pada suatu bidang koordinat. Dan grafik fungsi f f adalah grafik dari persamaan y = f (x) y = f ( x).

Persamaan Grafik Fungsi Kuadrat Pada Gambar Di Atas Adalah

Teorema ini biasanya membolehkan kita secara persis menentukan di mana suatu fungsi yang terdiferensialkan naik dan di mana ia turun. CONTOH 1: Jika f (x) = 2x3 −3x2 −12x +7 f ( x) = 2 x 3 − 3 x 2 − 12 x + 7, cari di mana f f naik dan di mana turun. Penyelesaian: Kita mulai dengan mencari turunan f f. Kita perlu menentukan di mana (x+1.

Cara Menggambar Grafik Fungsi Kuadrat kumpulan soal cat

Artinya terdapat x = a yang jika kita cari nilai limit mendakati a akan menghasilkan nilai + ∞ atau − ∞ (dimana a ≠ ∞) . Untuk fungsi aljabar, kondisi ini (memiliki asimtot tegak) jika fungsinya berbentuk pecahan. Fungsi y = f ( x) g ( x) memiliki asimtot x = a jika g(a) = 0 dan f(a) ≠ 0, artinya x = a adalah akar dari g(x) yang.

Cara Menentukan Persamaan Grafik Fungsi Trigonometri Foto Modis

Blog Koma - Setelah sebelumnya kita membahas materi menentukan fungsi eksponen dan fungsi logaritma dari grafiknya, kita lanjutkan dengan pembahasan materi Menentukan Fungsi Invers dari Grafiknya.Pada artikel ini kita akan lebih menekankan pada dua jenis grafik yaitu grafik fungsi eksponen dan grafik fungsi logaritma.Meskipun demikian, sebenarnya cara yang akan kita pelajari pada artikel ini.

Menentukan Fungsi dari suatu grafik trigonometri YouTube

Langkah-langkah Menggambar Grafik Fungsi. Menentukan titik stasioner dengan turunan pertama fungsi kurva f (x), f ′(x) = 0 f ′ ( x) = 0. Menentukan titik belok dengan turunan kedua fungsi kurva f (x), f "(x) = 0 f " ( x) = 0. Menentukan titik bantu di sekitar titik stasioner untuk mempertajam grafik.

Tentukan Persamaan Grafik Fungsi Trigonometri Di Bawah Ini Rumah Belajar

Hal unik yang perlu kita ketahui untuk sketsa dan menggambar grafik fungsi kuadrat yaitu grafik fungsi kuadrat berupa parabola dan arah atau hadap dari parabolanya tergantung dari nilai $ a \, $ nya. Nilai $ a \, $ dari fungsi kuadrat ini juga akan membantu kita untuk mengetahui jenis titik puncak dari grafik fungsi kuadratnya.Menggambar grafik fungsi kuadrat ini sangat penting karena biasanya.

Menentukan Persamaan Grafik Fungsi Eksponen Terbaru

Kesimpulan. Grafik fungsi merupakan representasi visual dari relasi antara input dan output fungsi matematika. Dengan membuat grafik fungsi, kita dapat lebih mudah memahami sifat-sifat dasar fungsi tersebut. Langkah-langkah untuk membuat grafik fungsi meliputi menentukan rentang nilai input, menghitung nilai output, memasukkan titik-titik hasil.

PErhatikan gambar berikut! Persamaan grafik fungsi kuadra...

A. Pengertian Fungsi (Function)Fungsi adalah istilah relasi khusus dalam ilmu matematika yang memetakan tepat satu-satu elemen himpunan daerah asal (domain) ke elemen himpunan daerah kawan (kodomain). Fungsi juga dikenal dengan istilah "pemetaan" karena setiap elemen daerah asal (domain) hanya berelasi sekali. Istilah fungsi dalam bahasa inggris disebut dengan "function".

13+ Contoh Soal Grafik Limit Fungsi Contoh Soal Terbaru

Blog Koma - Grafik fungsi kuadrat $ f(x) = ax^2 + bx + c \, $ disebut juga parabola karena lintasannya yang menyerupai parabola. Ternyata parabola $ f(x) = ax^2 + bx + c \, $ (di sini yang dimaksud adalah grafik fungsi kuadrat) memiliki beberapa karakteristik yang menarik untuk kita pelajari berdasarkan nilai $ a , \, b, \, $ dan $ c \, $ .

Cara Menentukan Rumus Fungsi Kuadrat Dari Grafik YouTube

Contoh 1: Menentukan Persamaan Kuadrat Jika Diketahui Gambar. #2: Diketahui Titik Puncak dan Titik Potong dengan sumbu - y. Contoh 2: Cara Menentukan Persamaan Kuadrat Jika Diketahui Gambar. #3: Diketahui Tiga Titik Sembarang pada Grafik Fungsi Kuadrat. Contoh 3: Soal Menentukan Persamaan Kuadrat Jika Diketahui Gambar.

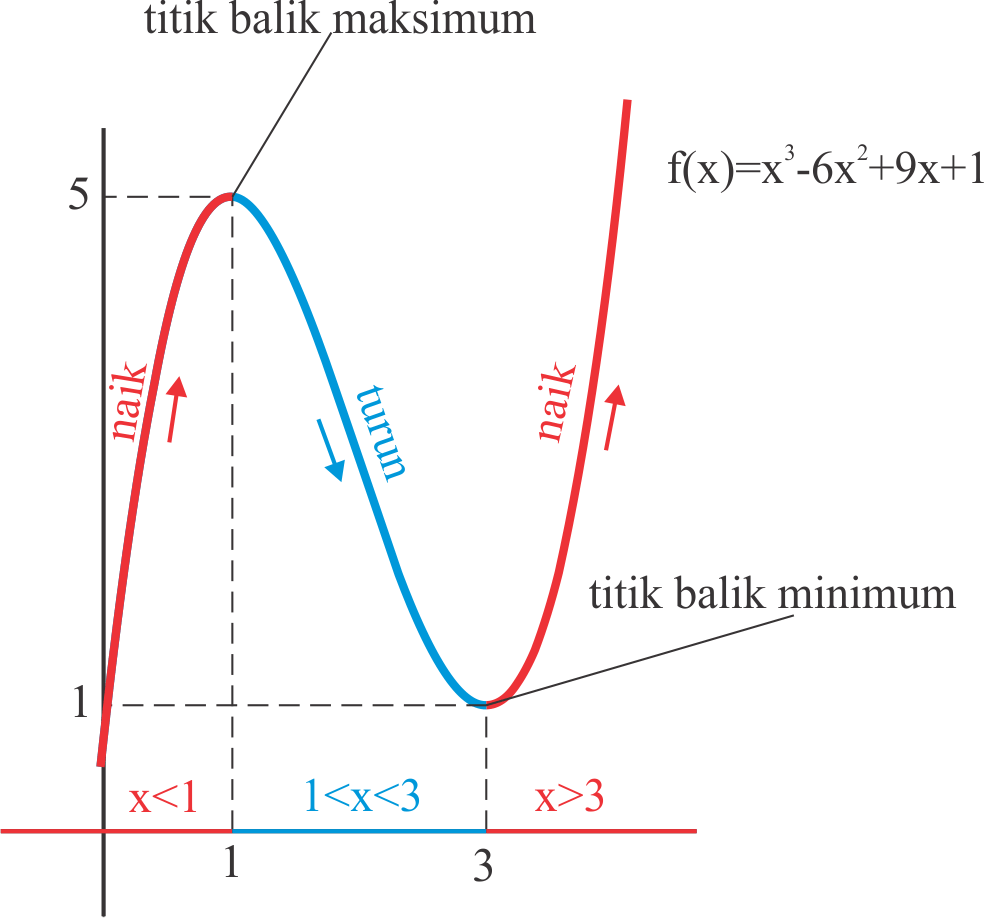
Menentukan Nilai Stasioner dan Jenis Ekstrim Fungsi Pada Matematika

Pelajari matematika dengan kalkulator grafik online kami yang bagus dan gratis. Gambarkan grafik fungsi dan koordinat, visualisasikan persamaan aljabar, tambahkan slider, animasikan grafik, dan banyak lainnya.

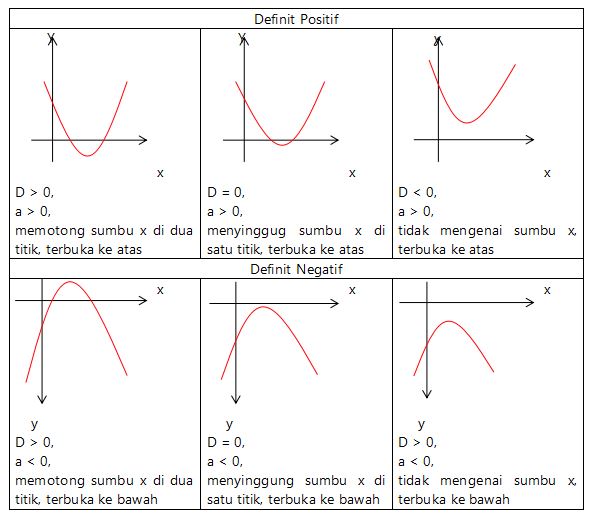
Persamaan Grafik Fungsi Kuadrat Pada Gambar Di Atas Adalah

Lima langkah pada cara menggambar grafik fungsi kuadrat adalah 1) mencari titik potong grafik dengan sumbu-x, 2) mencari titik potong grafik dengan sumbu-y, 3) menentukan letak sumbu simetri, 4) mencari titik-titik balik maksimum/minimum, dan 5) menghubungkan titik-titik yang diperoleh sehingga terbentuk sebuah parabola (seperti mebentuk huruf U).