Perhatikan Gambar Berikut Luas Yang Diarsir Adalah Tanya Tanya

Luas Lingkaran Bagian Yang Diarsir Pada Gambar Beriku vrogue.co

Unsur-Unsur Lingkaran. Unsur-unsur lingkaran ada 8 guys, yaitu titik pusat, jari-jari, diameter, tali busur, busur, juring, tembereng, dan apotema. Kita bahas satu per satu, ya! 1. Titik Pusat. Titik pusat adalah titik yang berjarak sama dengan semua titik pada keliling lingkaran. Letaknya tepat di tengah-tengah lingkaran.

Luas Daerah Lingkaran Yang Diarsir YouTube

Diketahui diameter sebuah lingkaran adalah 14 cm. Berapa luas setengah lingkaran tersebut? A. 38,5 cm² B. 77 cm² C. 115,5 cm² D. 154 cm². Pembahasan: Jari-jari= 1/2 diameter Jari-jari= 1/2 x 14 cm Jari-jari= 7 cm. Luas daerah yang diarsir = 1/2 x luas lingkaran Luas daerah yang diarsir = 1/2 π x r² Luas daerah yang diarsir = 1/2 π x 7²

Luas Daerah Yang Diarsir Pada Gambar Berikut Adalah analisis

Bangun datar di atas adalah ¾ bagian lingkaran dengan jari-jari (r) = 28 cm. Adapun rumus luas lingkaran: Luas lingkaran = = x (28cm x 28cm) = 22 x 4 cm x 28 cm =2.464 cm². Kemudian, kita kalikan luas tersebut dengan ¾. Luas daerah yang diarsir: = x luas lingkaran = x 2.464 cm² =3 x 616 cm² = 1.848 cm². Jadi, luas daerah yang diarsir.

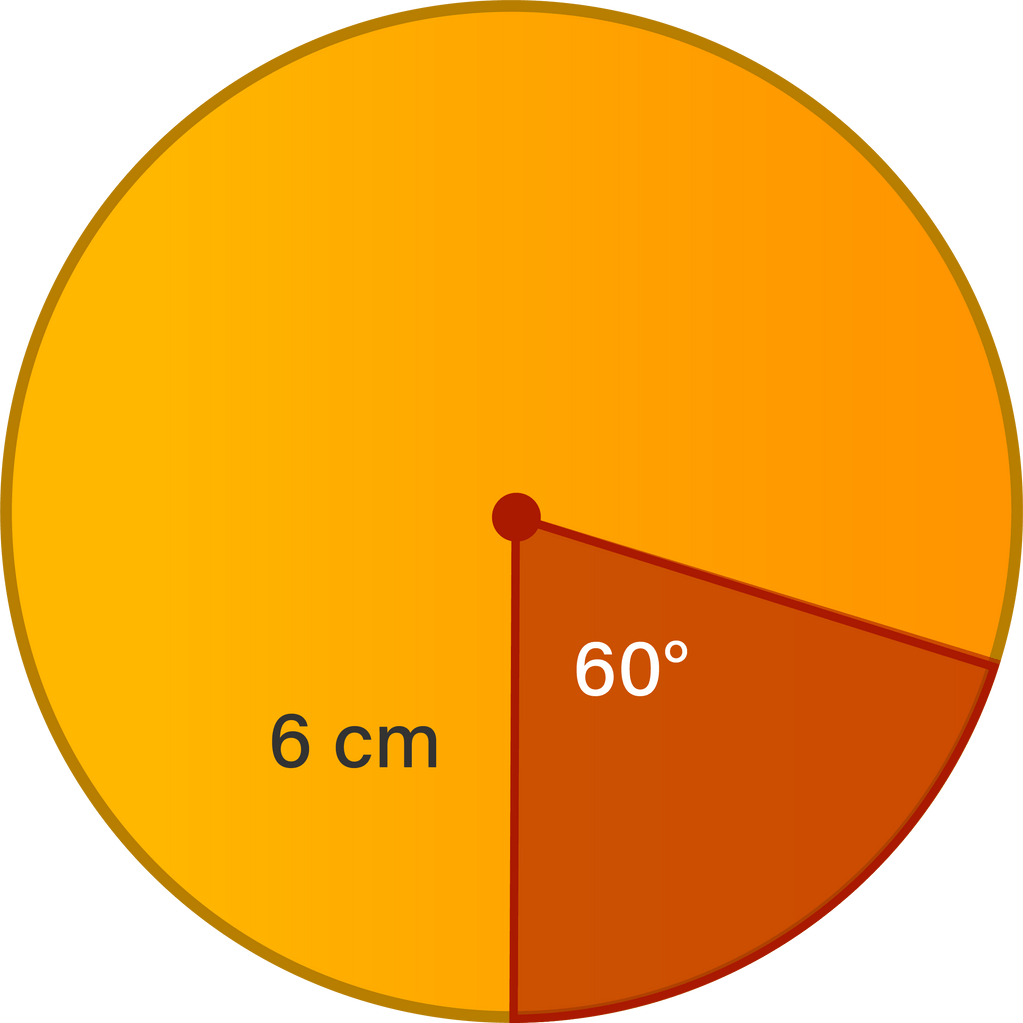
Luas daerah yang diarsir pada gambar berikut adala...

Soal dan Pembahasan Super Lengkap - Unsur, Keliling, dan Luas Lingkaran. Lingkaran sebenarnya bukan salah satu bangun datar sisi lengkung. Lingkaran adalah kumpulan titik-titik yang berjarak sama terhadap suatu titik tertentu (yang selanjutnya disebut sebagai titik pusat). Kita sering menemukan benda berbentuk lingkaran dalam kehidupan sehari.

Cara Mudah Menghitung Luas Bagian Lingkaran Yang Diarsir YouTube

Bagian yang diarsir adalah 2/4 lingkaran atau bisa disederhanakan menjadi ½ lingkaran.. Perhatikan gambar di bawah! Berapa luas yang diarsir pada gambar tersebut? a. 1.084 cm2. b. 1.232 cm2. c. 2.768 cm2. d. 3.022 cm2. Jawab: Bangun di atas adalah 4/8 lingkaran atau bisa disederhanakan menjadi ½ lingkaran.. Luas bangun berikut adalah.

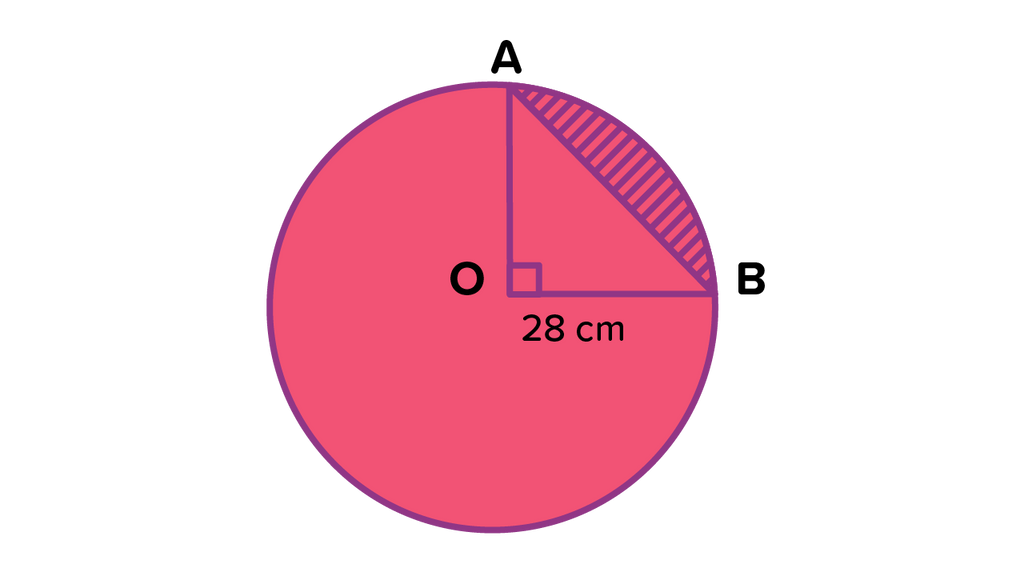
Luas daerah yang diarsir pada lingkaran berikut ad...

Untuk lebih jelasnya, dibawah ini diberikan beberapan contoh soal luas lingkaran dan pembahasannya. Contoh soal 1. Hitunglah luas lingkaran dengan jari-jari sebagai berikut: 7 cm. 21 cm. Pembahasan. Luas lingkaran soal 1 = π r 2 = 22/7 . (7 cm) 2 = 154 cm 2. Luas lingkaran soal 2 = 22/7 . (21 cm) 2 = 1386 cm 2. Contoh soal 2.

Luas Daerah Yang Diarsir Pada Gambar Berikut Adalah analisis

Rumus Luas Lingkaran. Cara Menghitung Luas Lingkaran bisa anda cari dengan : L = π.r.r . Dan penjelasan dari r ialah jari - jari lingkaran yang biasanya ada disetiap soal - soal yang membahas tentang materi diatas serta π sudah pasti menggunakan angka 3,14 atau bisa anda lihat rumus mencari luas lingkaran secara jelas seperti dibawah ini.

Cara Menghitung Luas Daerah Yang Diarsir Idschool Riset

Rumus luas lingkaran adalah phi dikali jari-jari lingkaran kuadrat. Untuk rumus selengkapnya cek ulasan berikut ini.. berikut ini rumus-rumus lingkaran: 1. Luas lingkaran (L) = πr2 atau π x r x r 2. Diameter lingkaran (d) = 2 x jari-jari = 2r. Penentuan nilai π menggunakan 22/7 atau 3,14 ditentukan ketika ada angka yang diketahui.

contoh soal keliling lingkaran yang diarsir Lingkaran persegi setengah rumus matematika perhatikan

Pada gambar tersebut 4 buah seperempat lingkaran sama saja dengan 1 buah lingkaran dengan jari-jari 7 cm. Maka luas bagian yang diarsir akan sama dengan luas segi empat dikurangi dengan luas lingkaran. Luas daerah yang diarsir = Luas segiempat - Luas Lingkaran = (sisi x sisi) - (µ x r^2) = (14 x 14) - (22/7 (7 x 7)) = 196 - (22/7 (49))

Cara Mudah Menghitung Luas dan Keliling Bangun yang Diarsir Part 3 YouTube

Hitunglah luas dan keliling daerah yang diarsir pada gambar berikut! Pembahasan: Perhatikan gambar di bawah! Luas daerah yang diarsir:. Luas daerah yang diarsir adalah luas lingkaran berjari-jari 120 m $-$ luas lingkaran berjari-jari 100 m. $\begin{align} LA &= 3,14.120^2 - 3,14.100^2\\

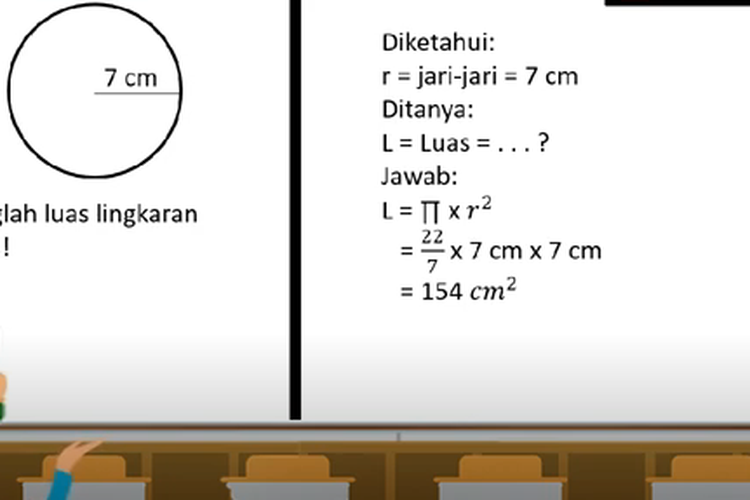
Contoh Soal Luas Lingkaran Homecare24

Untuk menyelesaikan tugas ini, kamu perlu memahami konsep dasar perhitungan luas dan mampu menerapkannya pada berbagai bentuk gambar. Dalam artikel ini, kita akan membahas cara menentukan luas daerah yang diarsir dari setiap jenis gambar, mulai dari persegi panjang, segitiga, lingkaran, hingga trapesium.

Cara Mudah Menghitung Luas Daerah Lingkaran Yang Diarsir YouTube

MATEMATIKA Soal dan Pembahasan MENGHITUNG LUAS YANG DIARSIR (LINGKARAN) MENGHITUNG LUAS YANG DIARSIR (LINGKARAN). Ini merupakan salah satu alternatif penyelesaian . Perhatikan gambar berikut. Berdasarkan gambar kita dapat menentukan luas daerah diarsir sebagai berikut. Luas daerah diarsis = Luas 1/4 lingkaran (r = 14) di kurang luas daearh I.

Luas Daerah Yang Diarsir Pada Gambar Berikut Adalah analisis

Penyelesaian: Luas daeah yang diarsir dapat dicari dengan cara mengurangi luas setengah lingkaran yang besar (berjari-jari 14 cm) dengan dua lingkaran yang luasnya setengah (berjari-jari 7 cm). Sekarang cari luas lingkaran yang besar, yakni: L. besar = ½ πr2. L. besar = ½ (22/7) (14 cm)2. L. besar = 308 cm2.

Cara Mudah Menghitung Luas Daerah Yang Diarsir Pada Bangun Datar (Soal Siswa) YouTube

Soal yang akan dibahas berikut ini adalah mengenai luas daerah yang diarsir dalam sebuah bangun datar. Jadi, pastikan kamu sudah mengetahui rumus luas bangun datar ya. Berikut beberapa contoh soal mengutip Buku Kumpulan 100 Soal dan Pembahasan Bangun Datar oleh Abdul Muntolib dan Rizki Wahyu Yunian Putra, MPd:

Luas bagian yang diarsir pada lingkaran berikut adalah cm² Universityku

Luas bangun yang diarsir = luas persegi - luas lingkaran = 196 - 154 = 42 cm persegi Jadi luas bangun yang diarsir adalah 42 cm persegi. 2. Hitunglah luas bagian bangun datar yang diarsir di bawah ini! Pembahasan. Perhatikan gambar bangun gabungan yang di samping! Di sana terdapat bangun persegi panjang dan dua buah bangun 1/2 lingkaran.

Luas bagian yang diarsir pada gambar berikut adalah Universityku

Hitunglah luas bagian yang diarsir (tembereng) pada lingkaran tersebut! Jawab: Diketahui jari-jari (r) pada lingkaran di atas adalah 14 cm, dengan sudut pusat juring 90 derajat. Lalu untuk mencari luas tembereng, jelas kita perlu mencari dahulu luas juring. Jadi, masukkan dulu rumus luas juring. LJ = x π x r 2. LJ = x x 14 x 14. LJ = x 22 x 2 x 14