SOAL MOMEN INERSIA BENDA PARTIKEL YouTube

Momen Inersia

Keterangan: I = momen inersia (kg.m 2). m = massa benda (kg) r = jarak partikel ke sumbu putar (m) Rumus Momen Inersia Pada Benda Tegar. Sebelumnya, telah dijelaskan bahwa keberadaan ukuran kelembaman ini selain dipengaruhi oleh massa dan jarak (seperti pada benda titik), juga dipengaruhi oleh bagaimana bentuk benda.

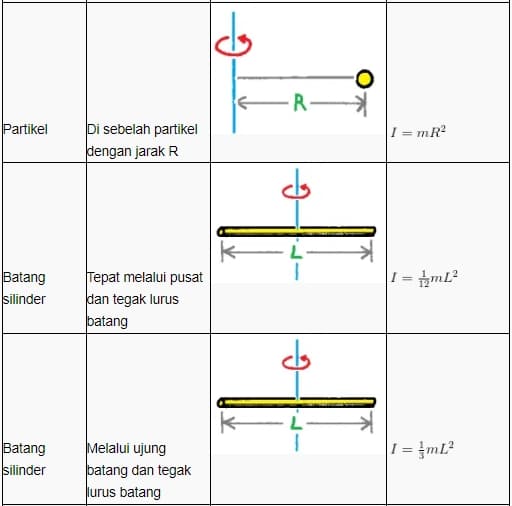
Pengertian Momen Inersia Rumus, Contoh dan Pembahasannya Pelajaran Sekolah Online

Untuk keping lingkaran, momen inersia untuk sumbu rotasi yang tegak lurus terhadap penampangnya (Gambar 5.3) ditunjukkan pada persamaan berikut : 2 2 1 Is MR (5.8) dimana M adalah massa keping dan R jari-jari silinder. Gambar 5.3. Keping lingkaran. Jika suatu keping lingkaran atau silinder berotasi pada sumbu rotasi yang

penjelasan momen inersia, menghitung momen inersia benda terhadap sumbu x dan y serta titik a

Dua bola dihubungkan dengan kawat yang panjangnya 6 m seperti pada gambar dibawah ini. Contoh soal momen inersia nomor 2. Massa kawat diabaikan dan kedua bola diputar dengan sumbu tegak lurus kawat pada bola m 1. Hitunglah momen inersia sistem bola. Penyelesaian soal. Diketahui: m 1 = 4 kg dan r 1 = 0 (karena m1 terletak di sumbu rotasi) m 2.

Menghitung momen inersia sistem pada sumbu x dan y YouTube

Materi yang dibahas dalam soal-soal ini adalah "dinamika dan keseimbangan benda tegar". Soal fisika kelas 11 ini diambil dari soal-soal uji kompetensi dalam buku Fisika untuk SMA/MA Kelas XI yang disusun oleh Marthen Kanginan dan diterbitkan oleh PT. Erlangga. Buku yang digunakan adalah buku yang disusun berdasarkan kurikulum 2013 dan.

Momen Inersia Rumus, Contoh Soal, dan Penjelasannya

Jadi Momen Inersia partikel merupakan hasil kali antara massa partikel itu (m) dengan kuadrat jarak tegak lurus dari sumbu rotasi ke partikel (r 2). Untuk mudahnya, bandingkan dengan gambar di atas. Secara matematis, momen inersia partikel dirumuskan sebagai berikut : I = mr 2. Keterangan : I = momen inersia. m = massa partikel

Momen Inersia Sistem Partikel Dinamika Rotasi Kelas 11 YouTube

Contoh Soal Momen Inersia 1. Empat buah partikel yang saling berhubungan dan membentuk satu sistem kesatuan dengan konfigurasi seperti gambar diatas. Masing-masing partikel memiliki berat yang berbeda dan jarak antar partikel satu sama lain sebesar R. Tentukan momen inersia sistem diatas jika: a.

SOAL MOMEN INERSIA BENDA PARTIKEL YouTube

Perhatikan gambar di bawah ini! Tiga buah partikel dengan massa m, 2m, dan 3m dipasang pada ujung kerangka yang massanya diabaikan. Sistem terletak pada bidang xy. Jika sistem diputar terhadap sumbu y maka momen inersia sistem adalah.. A. 5 ma. B. 7 ma. C. 5 ma 2. D. 6 ma 2. E. 7 ma 2. Pembahasan: I = ΣmR 2 = m 1 R 1 2 + m 2 R 2 2

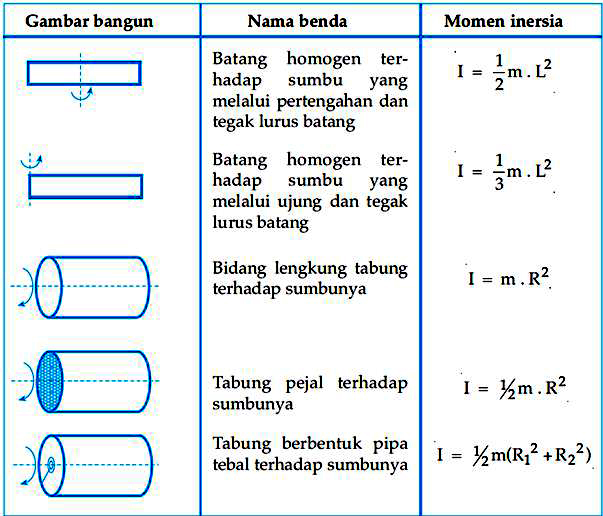
Pengertian dan Rumus Momen Inersia Lengkap Anto Tunggal

Momen inersia bola pejal dengan poros melalui pusat massa, dapat ditentukan dengan menggunakan sistem koordinat bola sehingga elemen massanya dapat ditulis sebagai berikut. dm = ρ dV. dm = ρ r 2 sin θ dr dθ dϕ (koordinat bola) r = r sin θ. dengan batas integrasi. r : 0 sampai R.

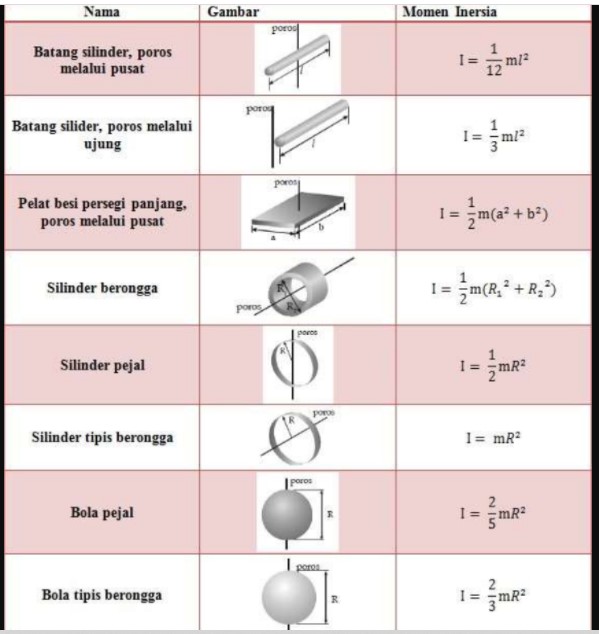
Momen Inersia (Pengertian, Rumus dan Kegunaannya)

Rumus Momen Inersia. Pada suatu partikel dengan massa m yang sedang berotasi pada sumbunya dengan jari-jari R. Momen inersia titik partikel tersebut bisa dinyatakan sebagai hasil kali massa partikelnya dengan jari-jarinya (jarak partikel ke sumbu putar). maka, momen inersia dapat dinyatakan dengan: I = m.R 2. Keterangan : I = Momen Inersia (Kg m 2)

Momen inersia sistem terhadap sumbu x dan y YouTube

Rumus momen inersia adalah rumus yang menghitung suatu besaran, dimana ada nilai tetap pada suatu gerak rotasi. Coba kamu perhatikan gambar dibawah ini: Benda dengan massa m yang mempunyai titik putar dengan jarak r, rumus momen inersianya akan dinyatakan seperti ini: I = mr 2. Keterangan: m = massa benda (kg) r = jarak benda pada sumbu putar.

Contoh Soal Momen Inersia Sumbu X Dan Y

Rumus momen inersia pelat tipis yang diputar di ujung. Suatu pelat bermassa M dan memiliki panjang a serta lebar b diputar di bagian ujung seperti gambar berikut. Momen inersia pelat segiempat tersebut dirumuskan sebagai berikut. Dengan: I = momen inersia (kg.m 2); M = massa pelat (kg); dan. a = panjang pelat (m). Rumus Momen Inersia Silinder

Tabel Momen Inersia Beberapa Benda Tegar Reverasite

Artikel Fisika kelas 11 ini membahas tentang konsep momen inersia, serta contoh penerapannya di kehidupan sehari-hari. —. Coba perhatikan mainan di atas deh. Benda-benda yang akan diluncurkan pada lintasan yang sama itu punya bentuk yang berbeda-beda. Mulai dari kotak, bola pejal (padat), bola berongga, silinder pejal, maupun silinder.

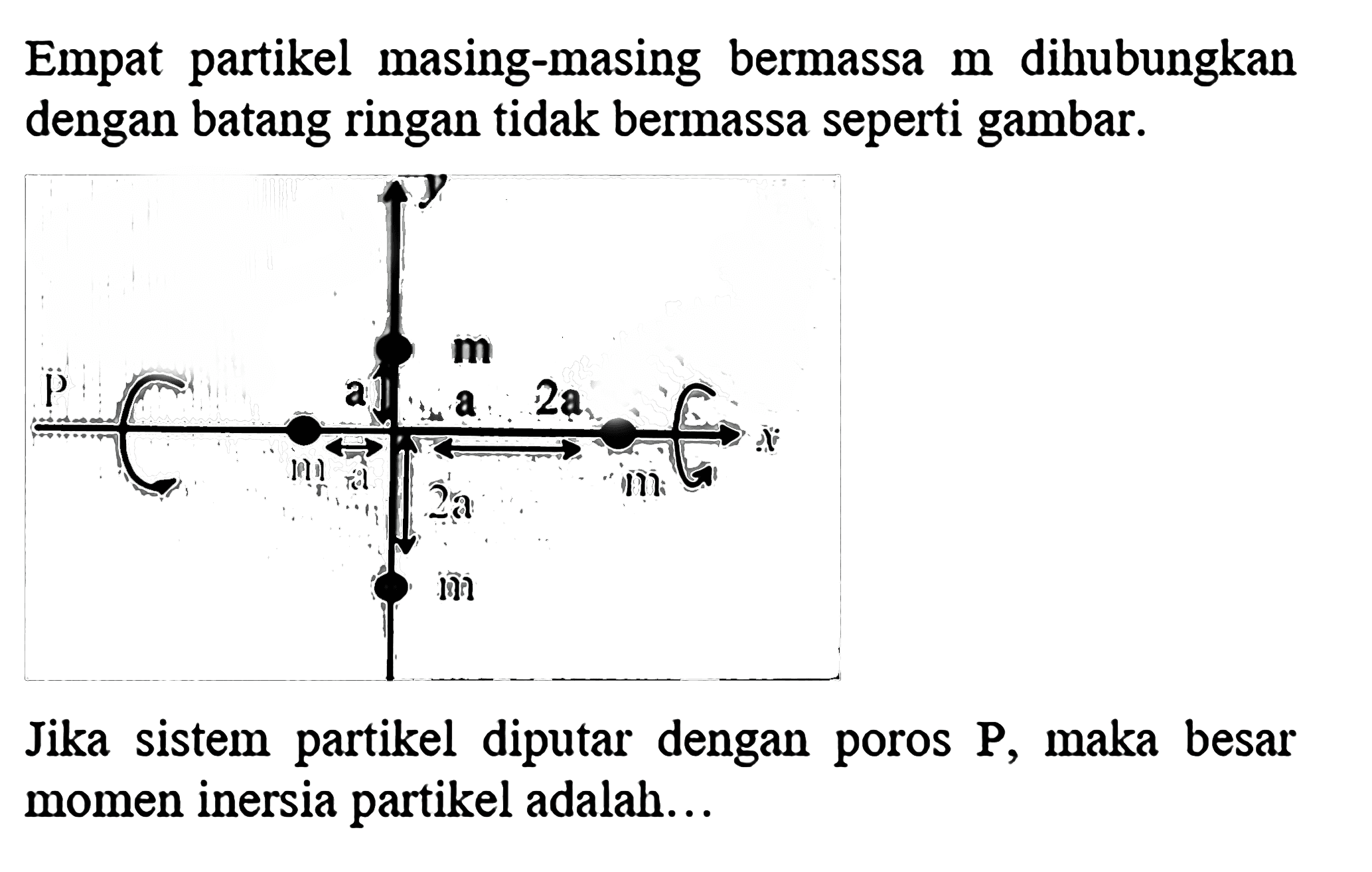
Hitunglah momen inersia dari batang yang massanya 2 kg be...

Selain untuk menyelesaikan momen inersia sistem partikel tunggal seperti penjelasan sebelumnya. Momen inersia juga menjelaskan untuk sistem partikel berjumlah banyak yang mana merupakan jumlah dari momeen inersia masing-masing komponen sistem partikel.. Bola bermassa 100 gram dihubungkan dengan seutas tali yang panjangnya 20 cm seperti pada.

Lihat Benda Beputar, Ingat Momen Inersia! Quipper Blog

Momen Inersia: Pengertian, Jenis, Rumus, Contoh Soal. December 5, 2023 by Mila. Momen inersia berbicara mengenai ukuran kelembaman suatu benda yang berputar terhadap porosnya. Bentuk benda yang berputar terhadap porosnya menentukan nilai momen inersia benda tersebut. Peloncat indah yang menekuk tubuh di udara adalah contoh momen inersia yakni.

MOMEN INERSIA PART 1 cara mudah memahami materi momen inersia partikel YouTube

Rumus Momen Inersia Partikel. I=mr 2. 2. Momen Inersia Benda Tegar. Momen inersia ini menganggap partikel tersebar menyeluruh di setiap bagian benda. Setiap partikel itu punya masa dan tentu saja memiliki jarak r dari suatu porosnya. Rumus Momen Inersia Benda Tegar. I=∑mr 2. Batang silinder (poros tengah) I=1/12mr 2. Batang silinder (poros.

Tabel Momen Inersia Beberapa Benda Tegar Reverasite

Momen inersia - Keilmuan Sains mengajak manusia mengenali struktur alam yang rumit dan kompleks untuk pada akhirnya bisa disederhanakan. Sains lalu senantiasa mengembangkan dirinya dari masa ke masa. Menemukan pembacaannya untuk ke sekian kali pada bentuk dan ukuran, bahkan hitungan tertentu yang bisa dikenali manusia.