Belajar Kongruen Dan Kesebangunan Bangun Datar

7 Contoh Soal Bangun Datar Terbaru Kolektor Soal 28

Pengertian kesebangunan seperti ini berlaku umum untuk setiap bangun datar. Dua bangun datar dikatakan sebangun jika memenuhi dua syarat berikut: Panjang sisi-sisi yang bersesuaian dari kedua bangun itu memiliki perbandingan senilai. Sudut-sudut yang bersesuaian dari kedua bangun itu sama besar. Untuk memantapkan pemahaman Anda tentang.

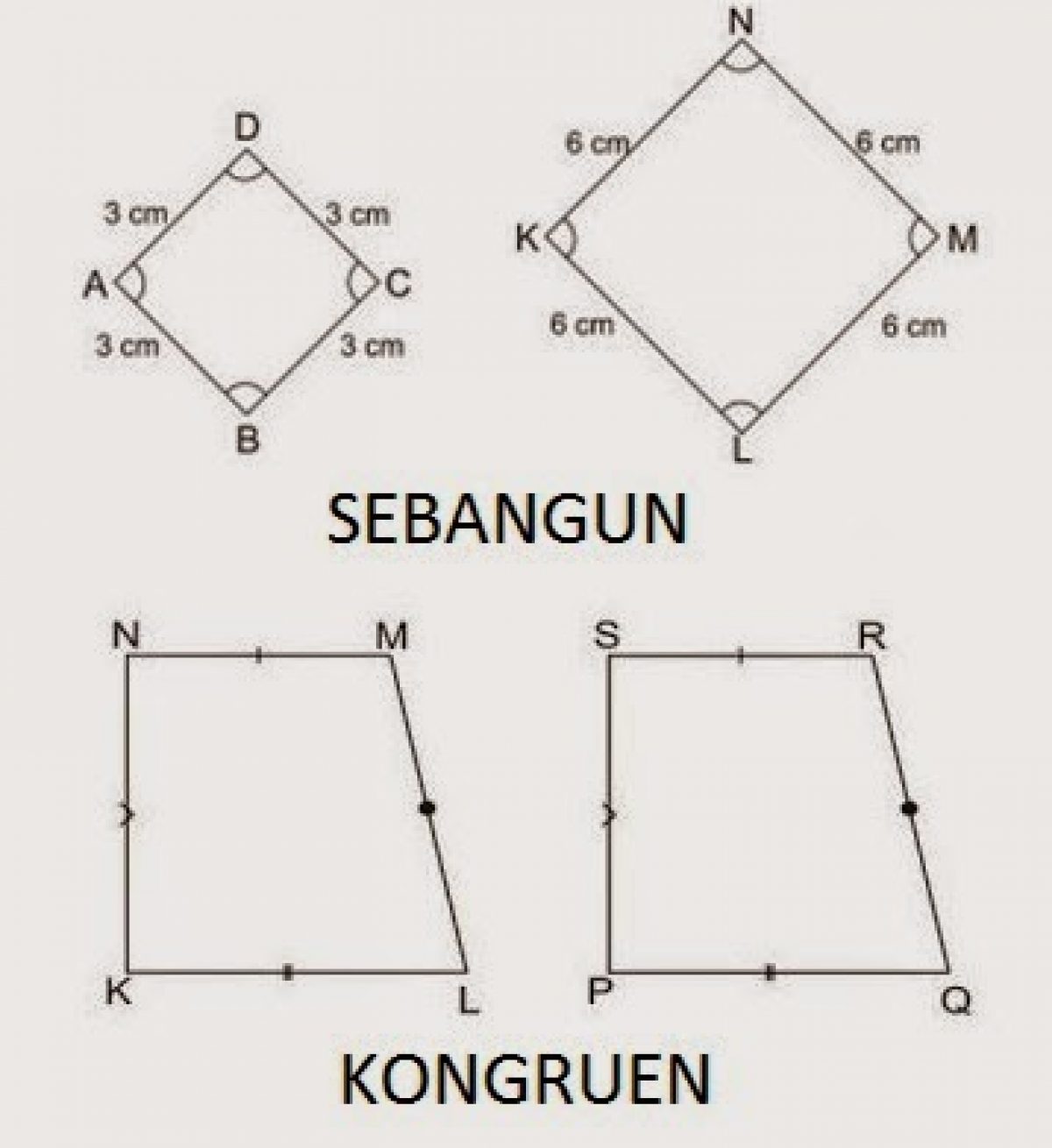
Apa Yang Di Maksud Dengan Sebangun Dankongruen? Contoh Soal Matematika Kelas 9

Rumus Kesebangunan dan Contoh Soalnya. Jika ada soal seperti di atas, maka cara pengerjaannya adalah sebagai berikut : Kita bandingkan dulu sisi-sisi dari dua bangun datar persegi panjang tersebut, yaitu. PQ/AB = PS/AD. PQ/16 = 6/4. PQ = 16×6/4.

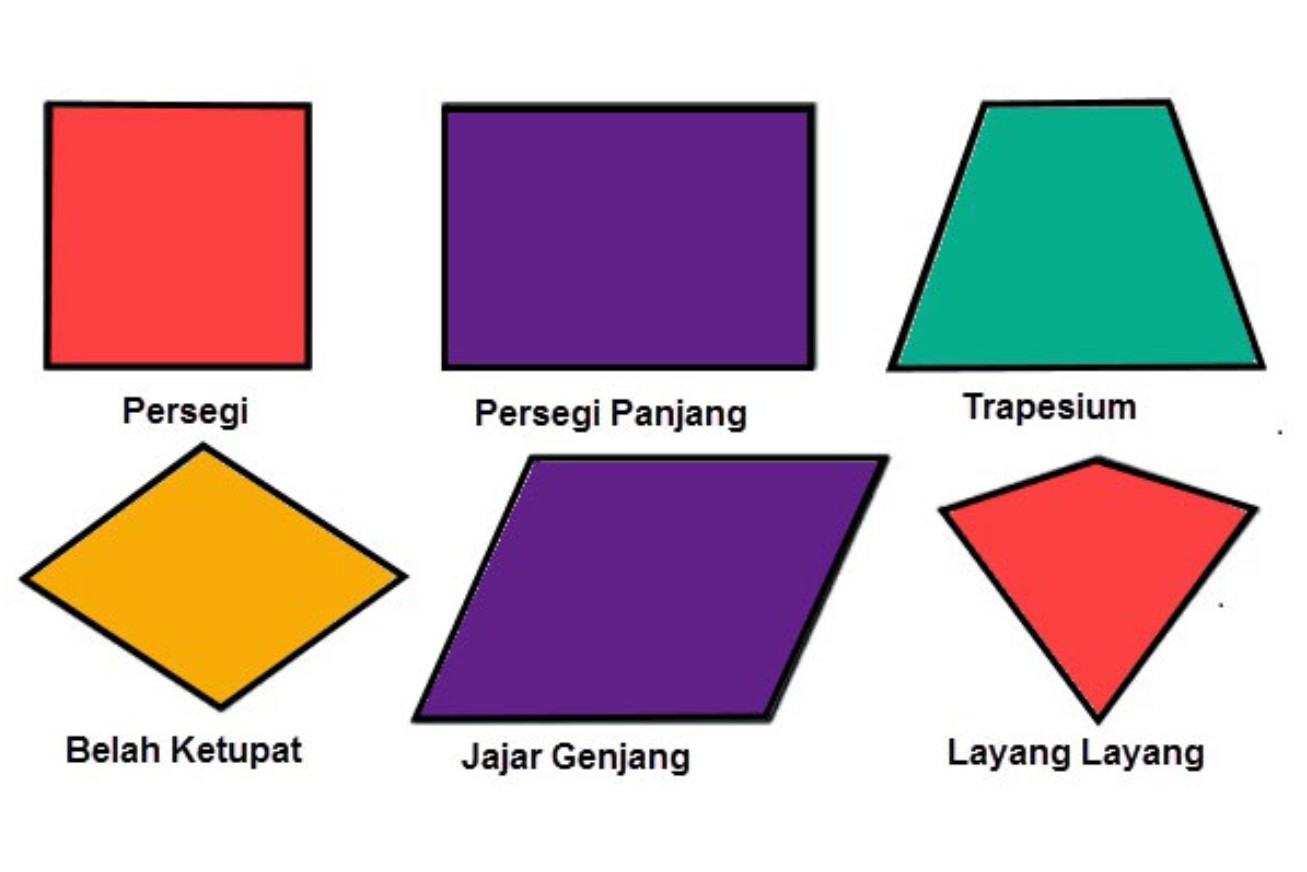
Mengenal Bentuk Bangun Datar Dan Ciri Cirinya Materi Kelas Sd Tema Sexiz Pix

Dalam penulisannya, kesebangunan umumnya dilambangkan dengan simbol notasi ≈. Perhatikan contoh gambar di bawah ini untuk lebih jelasnya. Dua Bangun Datar yang Sebangun. Kedua bangun tersebut adalah dua bangun yang sebangun dengan beberapa sifat yang sama. Syarat dua bangun datar dikatakan kongruen adalah sebagai berikut. 1. Perbandingan Sisi.

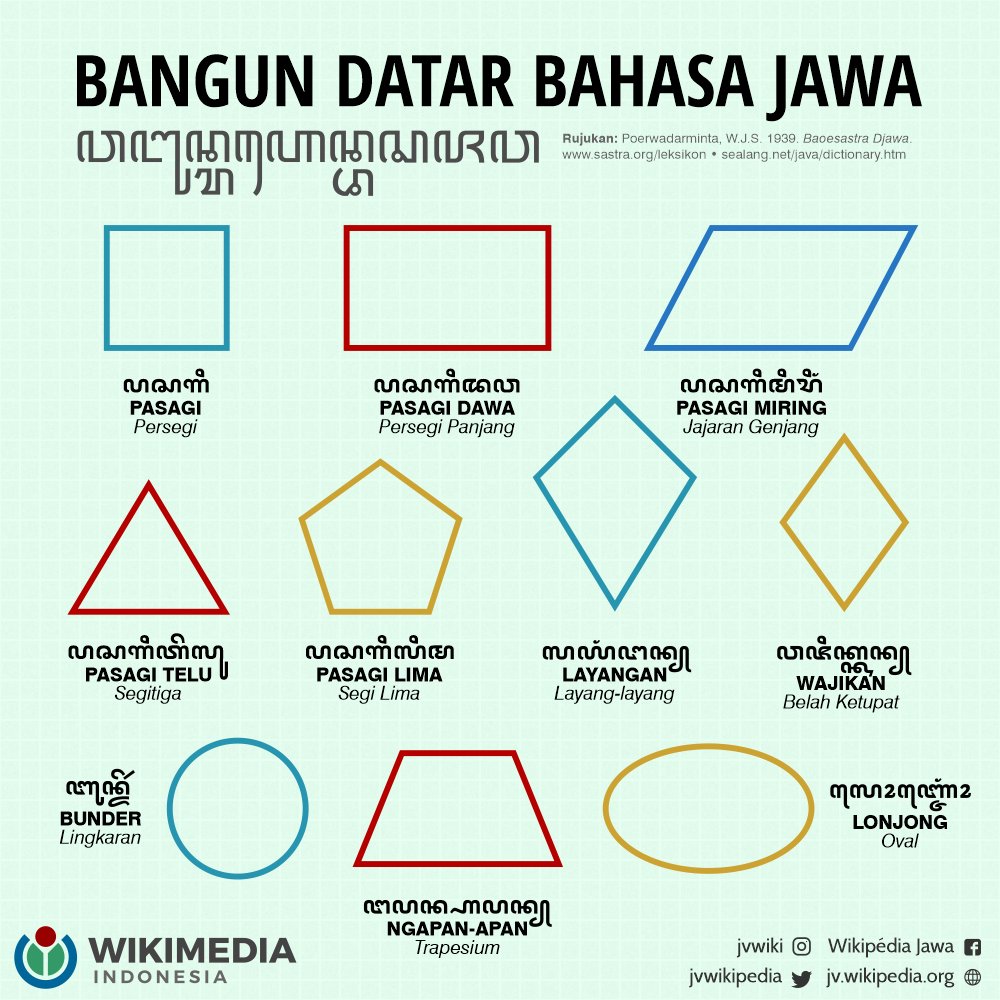
Nama Nama Bangun Datar Dan Gambarnya kabarmedia.github.io

Dua bangun datar dikatakan sebangun bila memiliki sisi yang sebanding dan sudut-sudut yang bersesuaian sama besar.. Ayo kita selidiki bersama dengan contoh kesebangunan dalam kehidupan sehari-hari! Pasfoto ukuran 2 x 3 dan ukuran 3 x 4. Pembuktian Rumus Jajargenjang dengan Persegi Panjang. Caranya kita tentukan perbandingan antara lebar.

Kesebangunan Bangun Datar

Dengan demikian, bangunnya menjadi sebagai berikut. Bangun awal dan bangun baru adalah bangun yang sebangun dengan perbandingan 1 : 3. Asyiknya Mencoba. A. Perhatikan gambar berikut! Gambarlah dengan ukuran lebih besar. Perbandingan ukuran awal : ukuran baru = 1 : 10. 1. 30 cm x 20 cm. 2. 20 cm x 20 cm. 3. 30 cm x 20 cm.

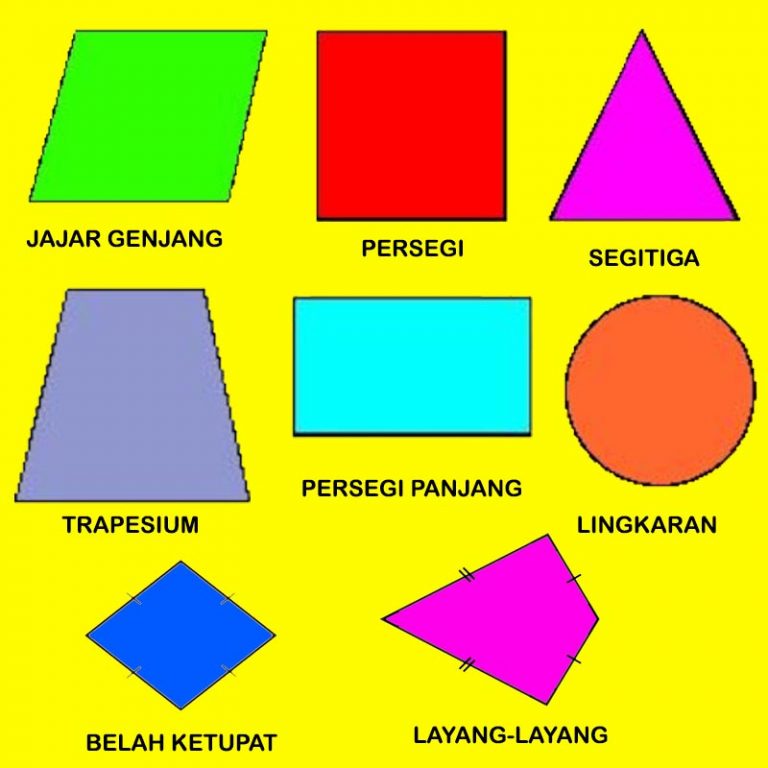
Bangun Datar Pengertian Macam Macam Sifat Sifat Dan Rumus Bangun Hot Sex Picture

Untuk rumus dari perbandingan kedua bangun datar tersebut bisa diidentifikasikan seperti ini: Panjang AB = 36 cm, Panjang EF = 18 cm, Panjang BC = 12 cm, Panjang FG = 6 cm. Sehingga, EF/AB= 18/36= 1/2. BC/FG= 12/6= 1/2. Sehingga dapat dikatakan bahwa, jika terdapat dua persegi panjang yang sebangun, berlaku rumus:

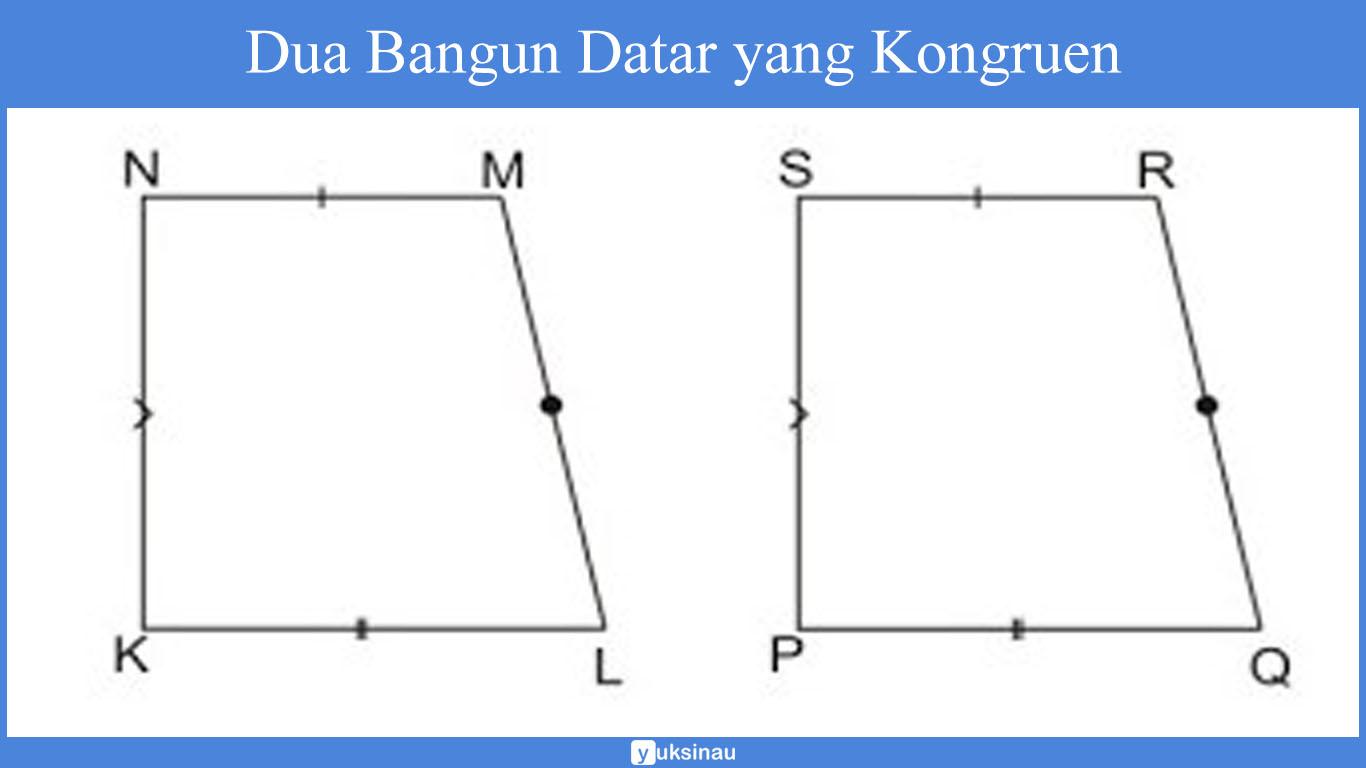
MATEMATIKA SANGAT ASYIK KESEBANGUAN DAN KEKONGRUENAN DUA BANGUN DATAR

Prinsip kesebangunan dimanfaatkan pada perbesaran foto dan pembuatan model benda. Dua bangun datar yang sebangun. Sifat-sifat yang dimiliki: Pasangan sisi yang bersesuaian memiliki perbandingan panjang yang sama. Besar sudut yang bersesuaian sama besar. Sumber gambar: Buku BSE kelas 9 Matematika. Dua segitiga yang sebangun.

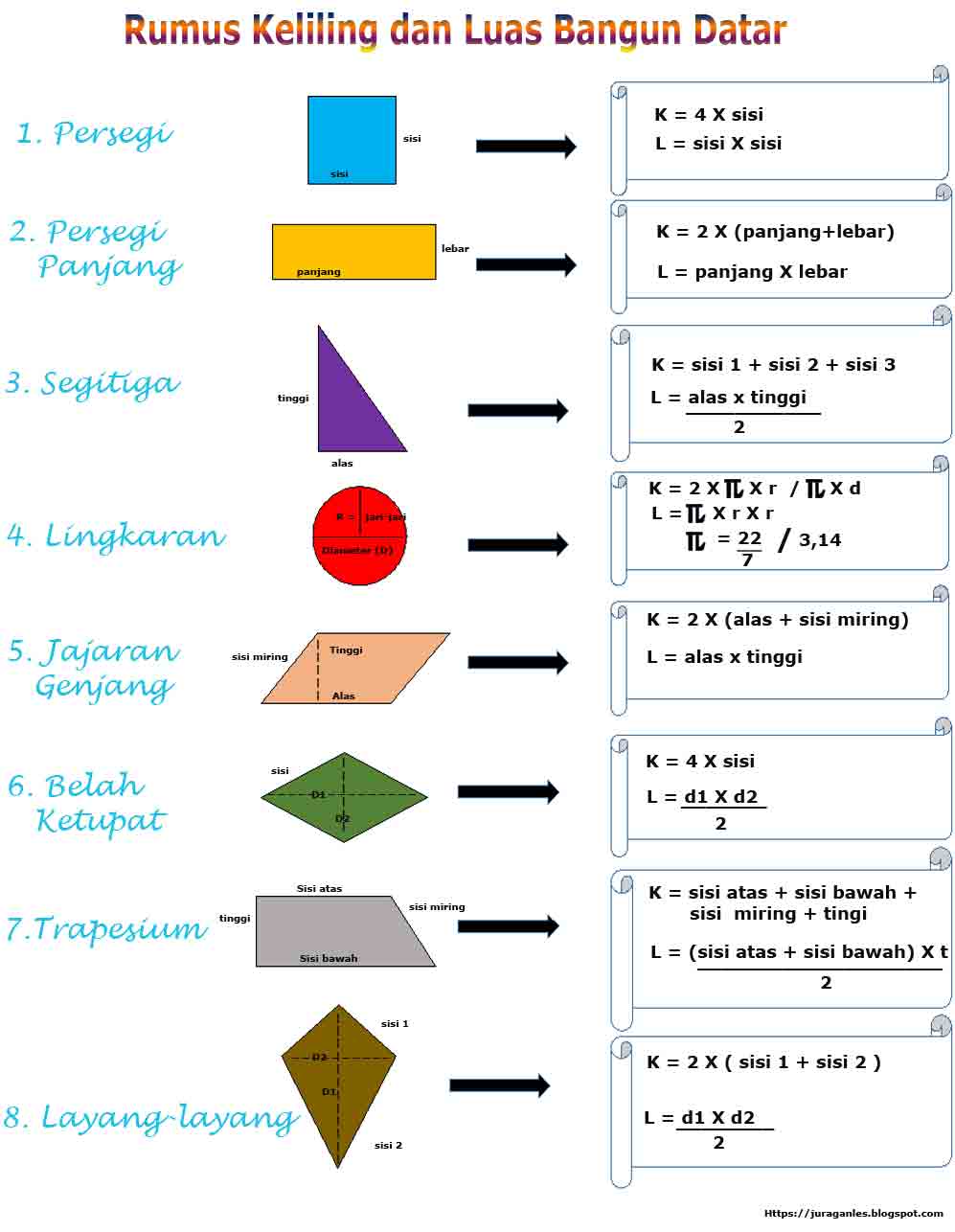
Gambar Bangun Datar Dan Rumus

Dalam kehidupan sehari hari kita lihat beberapa benda yang kongruen seperti keramik rumah, lembar kertas pada buku. Berikut adalah contoh dari bangun-bangun yang kongruen. Gambar (1) dan 2, (3) dan (4), (5) dan (6) meruapakan gambar yang memiliki bentuk dan ukuran yang sama. Gambar (2) merupakan hasil gambar (1) yang diputar 45 ̊gambar (1.

Konsep Bangun Datar, Kesebangunan, dan Kongruensi Segitiga Sekolah Dasar YouTube

Materi kesebangunan dan kekongruenan mulai diajarkan pada SMP kelas 9 yang membahas mengenai konsep kesebangunan pada bangun datar serta penggunaan konsep ini dalam memecahkan masalah. Dengan memahami konsep ini, maka bisa diidentifikasi bangun datar yang kongruen dan sebangun.. Contoh bangun persegi panjang yang saling sebangun tampak di.

Belajar Asik Dan Kreatif KUMPULAN SOAL DAN KUNCI JAWABAN KESEBANGUNAN DAN KEKONGRUENAN BANGUN

Kekongruenan dan kesebangunan memang terlihat mirip, namun juga memiliki beberapa perbedaan. Untuk memahami dengan lebih baik, kamu bisa membaca penjelasan di bawah ini. Pengertian Kongruen. Secara sederhana, bangun datar kongruen adalah istilah yang digunakan untuk menyatakan dua objek bangun datar yang sama persis. Baik secara ukuran, sudut.

MacamMacam Bangun Datar Dan Gambarnya Cilacap Klik

Perbandingan ini dinamakan dengan faktor skala atau rasio. Dapat disimpulkan, dua bangun datar dikatakan sebangun bila memenuhi dua syarat sebagai berikut: Sudut-sudut yang bersesuaian sama besar; Sisi-sisi bersesuaian memiliki perbandingan sama. Untuk memahami konsep kesebangunan bangun datar, simak dua contoh soal di bawah ini: Contoh Soal 1.

Inilah Syarat Dua Bangun Datar Dinyatakan Sebangun Beserta Contoh Gambarnya

Contoh Gambar. Ciri-ciri. - sisinya ada 4 (a) - memiliki diagonal (d) - setiap sudutnya sebesar 90°. - total sudutnya 360°. 2. Bangun Persegi Panjang. Bangun datar persegi panjang merupakan bangun datar serupa persegi tapi panjang seluruh sisinya tidaklah sama, sehingga membuatnya mempunyai panjang (p) dan lebar (l).

10 Rumus Bangun Datar Luas, Keliling dan Contoh Soal

Ada dua bangun datar atau lebih yang pasti sebangun, di antaranya: Lingkaran. Contohnya: Perbesar. Lingkaran kesebangunan (Dok. Supriaten) Lingkaran memiliki besar ∠360°. Panjang jari-jari dan. Gambar di atas memenuhi syarat kesebangunan, sehingga dua buah lingkaran tersebut merupakan dua bangun yang sebangun.

Bangun Datar Kelas 4 SD/MI Keliling Bangun Datar Semester 2 Kurikulum 2013 YouTube

Rumus Persegi - Luas, Keliling, Ciri-Ciri, dan Contoh Soal. Halo Sobat Zenius! Kali ini aku akan ngenalin kamu dengan bangun datar persegi termasuk cara menggunakan rumus keliling dan rumus luas persegi. Materi rumus luas dan rumus keliling persegi ini juga akan kamu temui di kelas 4 SD. Dan kalo kamu liat sekeliling, ternyata banyak lho.

Belajar Kongruen Dan Kesebangunan Bangun Datar

Berikut contoh soal materi kesebangunan bangun datar persegi panjangnya yaitu: Poster yang ukurannya 24 cm x 29 cm terletak di atas bingkai karton yang ukurannya sebangun. Jika kanan, kiri, dan atas sisinya tersisa 12 cm. Berapakah besar sisa pada bagian bawah sisi bingkainya? Jawab. Untuk menyelesaikan contoh soal kesebangunan bangun datar.

Kesebangunan dan kekongruenan YouTube

Kesebangunan dan kekongruenan pada bangun datar sendiri termasuk dalam kategori ilmu Geometri Matematika. Dua buah bangun datar dapat dinyatakan sebangun jika sisi sisi keduanya mempunyai kesamaan dalam perbandingan nilainya. Kemudian dua buah bangun datar dapat dinyatakan kongruen jika mempunyai persamaan dalam besar sudut dan bentuk ukurannya.