Треугольник Паскаля — презентация

Треугольник Паскаля online presentation

В ролике обсуждаются основные арифметические и комбинаторные свойства треугольника Паскаля — одной из самых изящных конструкций в математике, играющей исключ.

Бином Ньютона, треугольник Паскаля и Яндекс Практикум по математике Артур Рыкалин Дзен

В математике треугольник Паскаля является треугольным массивом из биномиальных коэффициентов. Он назван в честь французского математика Блеза Паскаля, хотя за много веков до него другие учёные уже изучали эту фигуру. Например, одни из первых упоминаний обнаружены в Индии, Персии (Иран), Китае. Содержание: Основная формула История открытия

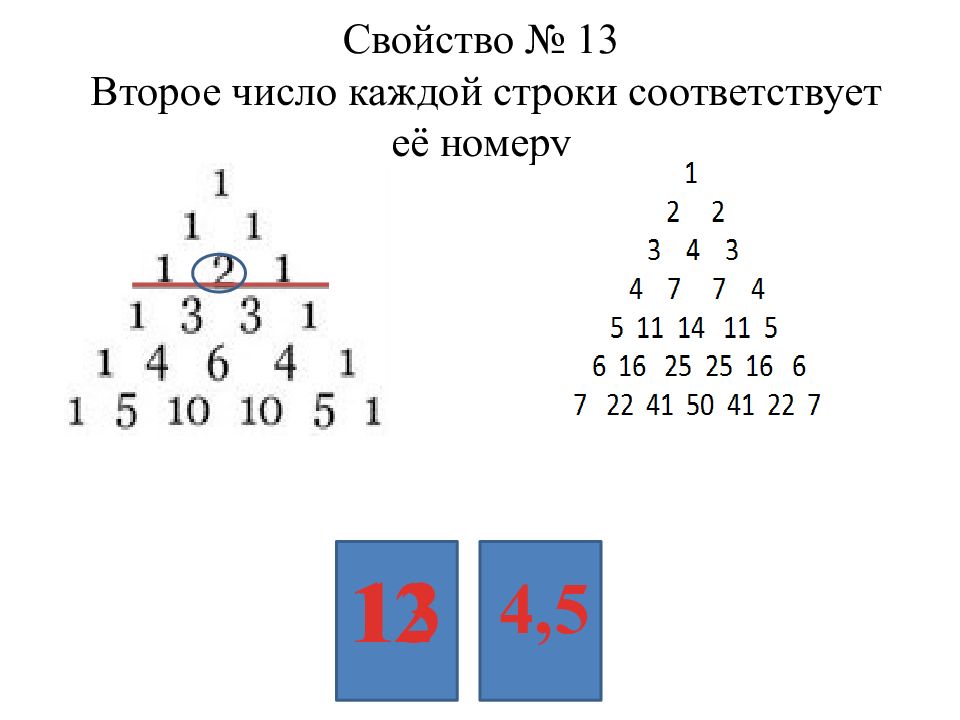
Треугольник Паскаля — презентация

Треугольник Паскаля можно получить из таблицы натуральных степеней бинома x + y .. Каждое число в треугольнике Паскаля равно C n k, где n - номер строки, k - номер.

Химический сдвиг. ЯМРспектроскопия презентация онлайн

Треугольник Паскаля - Последовательности и паттерны - Mathigon Треугольник Паскаля Ниже вы можете увидеть числовую пирамиду, созданную с использованием простого шаблона: она начинается с единственной «1» в вершине, а каждая следующая ячейка является суммой двух ячеек, расположенных непосредственно выше.

Треугольник Паскаля online presentation

Треугольник Паскаля - равнобедренный треугольник, у которого на вершине и по бокам стоят единицы. Каждое число в нем равно сумме двух, расположенных над ним чисел. Строки треугольника Паскаля симметричны относительно вертикальной оси. Продолжать треугольник можно бесконечно. где n - натуральное число и: Построение треугольника Паскаля

Дополнительные задачи — Step 1 — Stepik

Треугольник Паскаля — это треугольный массив чисел, за которым следует определенный шаблон и соединение со строкой перед ним. Его изобрел Блез Паскаль. Этот треугольник начинается с одного элемента в первой строке. После этого каждая строка начинается и заканчивается цифрой «1». Содержание: Что такое треугольник Паскаля?

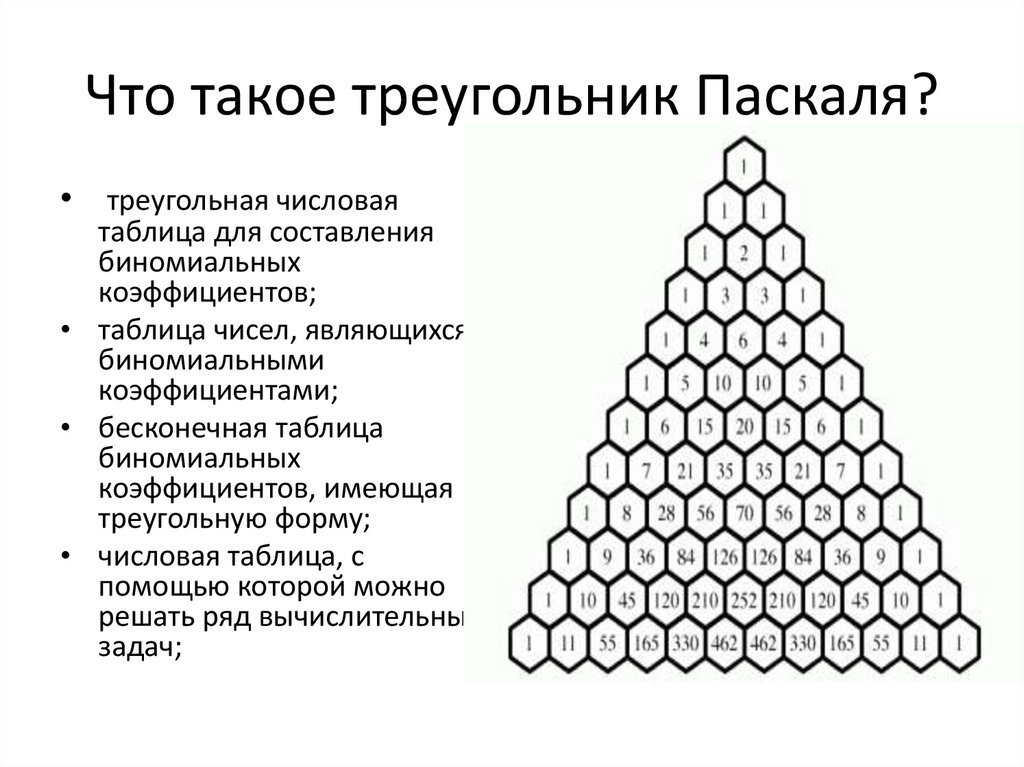
Треугольник Паскаля online presentation

Если раскрасить нечётные числа в треугольнике Паскаля в один цвет, а чётные — в другой, получится такая картина (на рисунке 10.1. «Треугольник Паскаля — Серпинского» указанным образом раскрашены числа в первых 128.

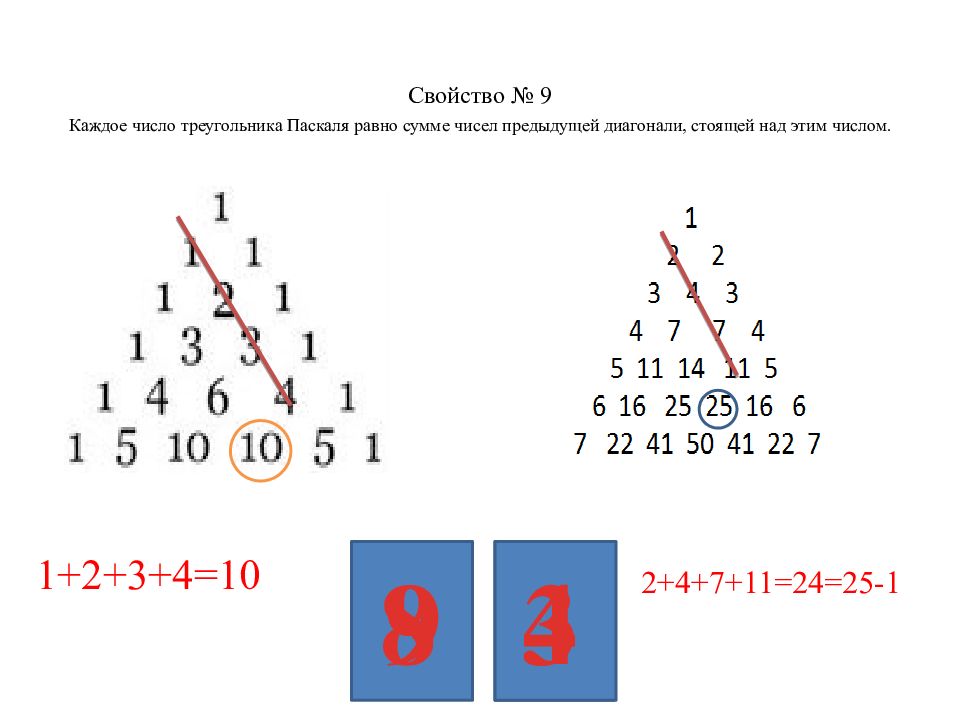
Треугольник Паскаля — презентация

Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом.

Треугольник Паскаля online presentation

In mathematics, Pascal's triangle is a triangular array of the binomial coefficients arising in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in Persia, [1] India, [2] China, Germany, and Italy. [3]

Треугольник Паскаля — презентация

Определение Треугольник Паскаля — форма записи биномиальных коэффициентов в виде бесконечной треугольной таблицы. Элементы массива обозначаются , где n — номер строки, k — порядковый номер элемента в строке. Нумерацию строк начинают с нулевой, при этом нулевая строка — это вершина, то есть число 1.

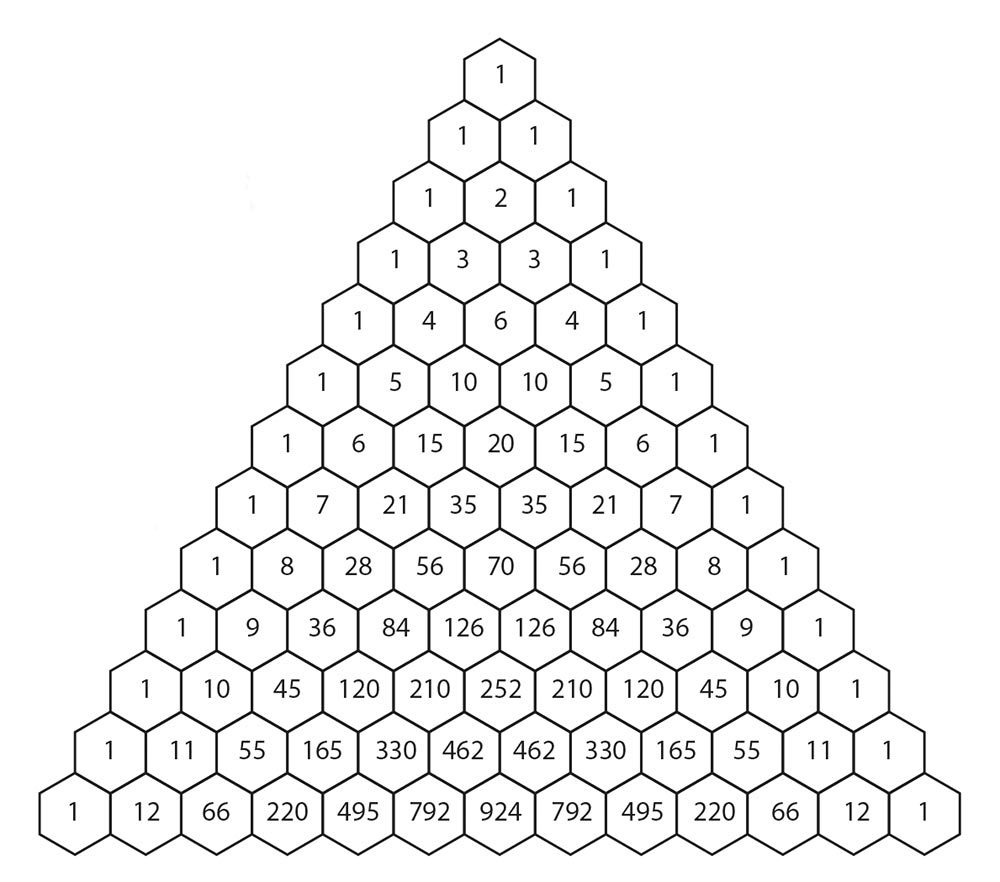
Треугольник Блеза Паскаля

Треугольник Паскаля ( арифметический треугольник ) — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.

Треугольник Паскаля online presentation

Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.

Треугольник Паскаля — презентация

1 ответ Сортировка: 1 for (int j = 1; j <= i*2+1; j++) { printf ("%d ",j); } for (int j = i*2+1; j >= 1; j--) { printf ("%d ",j); } У Вас пропущены нечетные строки. Поделиться Улучшить ответ Отслеживать изменён 16 окт 2018 в 16:25 ответ дан 16 окт 2018 в 16:20 user176262 Добавить комментарий Ваш ответ Отправить ответ

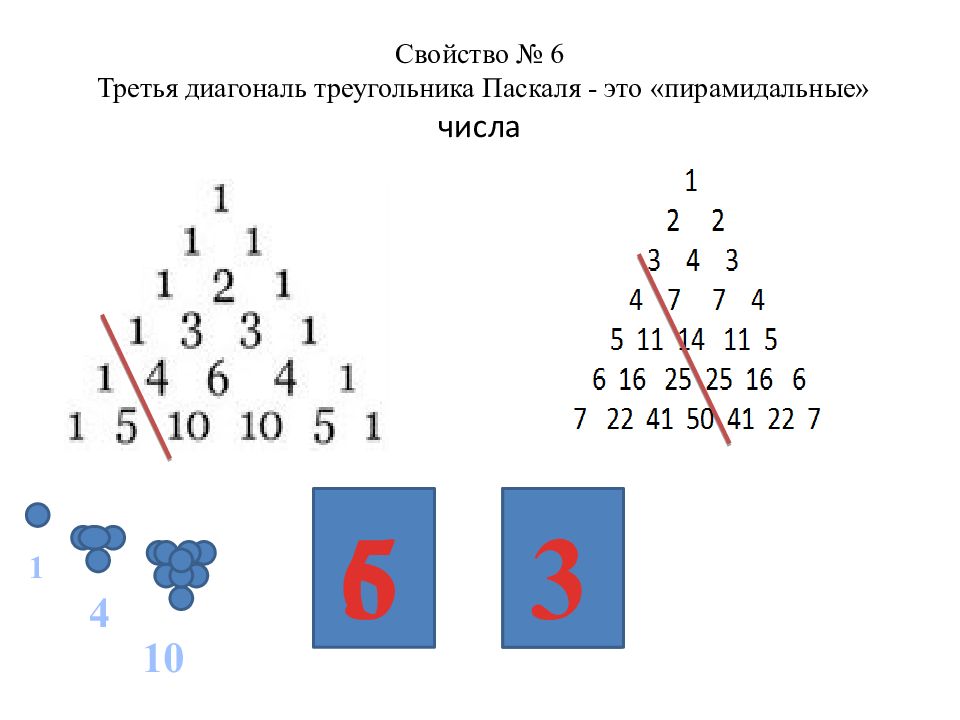
Треугольник Паскаля — презентация

1. Треугольник Паскаля Теория: Для любых значений n и m (0 ≤ m ≤ n) действительно равенство Cmn = Cn−mn. Зная данное свойство, можно ускорить решение задач. Пример: в магазине 7 разных маек. Галя хочет примерить 2 майки, а Аня хочет примерить 5. Сколько существует возможностей для каждой из девочек каждый раз выбрать новый комплект для примерки?

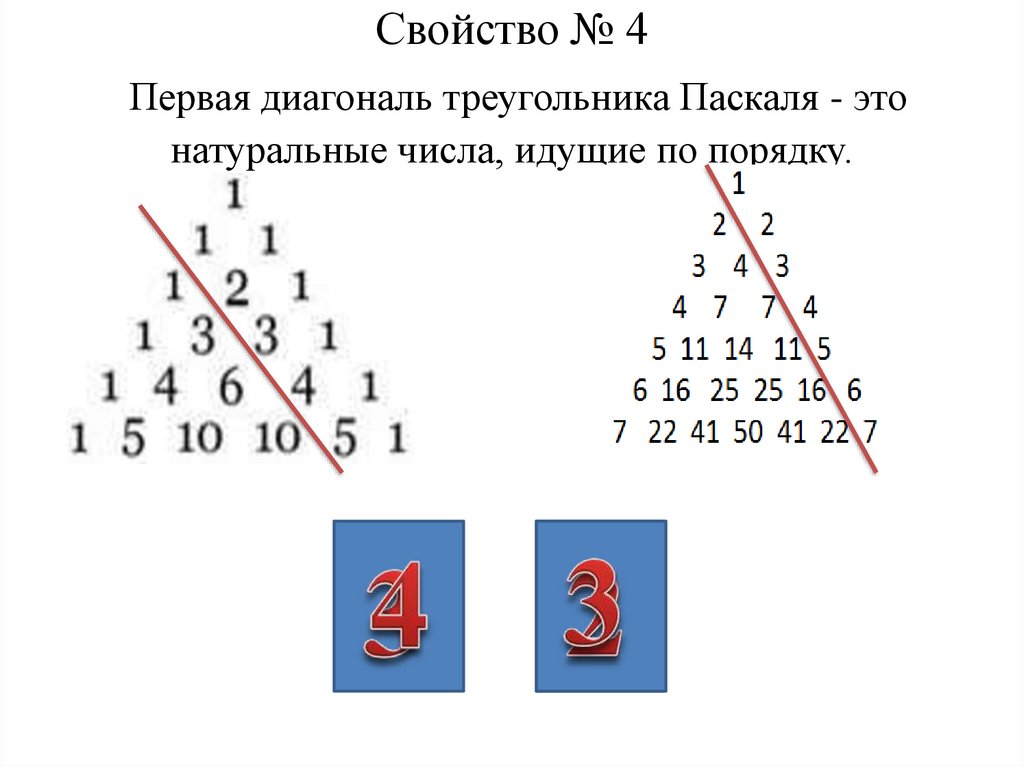
Треугольник Паскаля online presentation

Что такое треугольник Паскаля, как он составляется и какие удивительные закономерности в себе таит? Какие.