Blog matematyczny Minor Matematyka Mnożenie logarytmów

Zadanie 11 Zapisz liczby w postaci potęg o tej samej podstawie i
Dwa logarytmy o takiej samej podstawie dodajemy korzystając ze wzoru: loga b +loga c =loga(b ⋅ c) Z bardzo podobnego wzoru korzystamy, gdy chcemy odjąć logarytmy o wspólnej podstawie: loga b −loga c = loga(b c) Przykład 1. Oblicz log2 2 +log2 8. Rozwiązanie: log2 2 +log2 8 = log2(2 ⋅ 8) =log2 16 = 4 Przykład 2. Oblicz log2 2 −log2 8. Rozwiązanie:

Logarytmy. Zamiana podstawy logarytmu. Proszę o wytłumaczenie i
Sprawdź z jakich wzorów i własności można skorzystać na mnożenie, dzielenie, dodawanie, odejmowanie logarytmów o tych samych i różnych podstawach. Dowód działania 7, 8, 9, 10 Wiesz jak obliczyć x, y, z korzystając w podanych własności i działań na logarytmach? Sprawdź Post nr 491 Autor: Robert Karolewski o 15:49

Zastosowanie wzoru na zmianę podstawy logarytmu YouTube
Potęgi o tej samej podstawie dzielimy według wzoru: am:an =am−n lub równoważnie: am an = am−n Przykład 1. 36:32 = 36−2 = 34 Można to rozpisać tak: 36:32 = 36 32 = 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 3 ⋅ 3 = 3 ⋅ 3 ⋅ 3 ⋅ 3 = 34 Przykład 2. 57 53 =57−3 = 54 Przykład 3. (1 2)10 (1 2)4 =(1 2)10−4 = (1 2)6 Przykład 4. 10100 10300 = 10100−300 =10−200 Przykład 5.
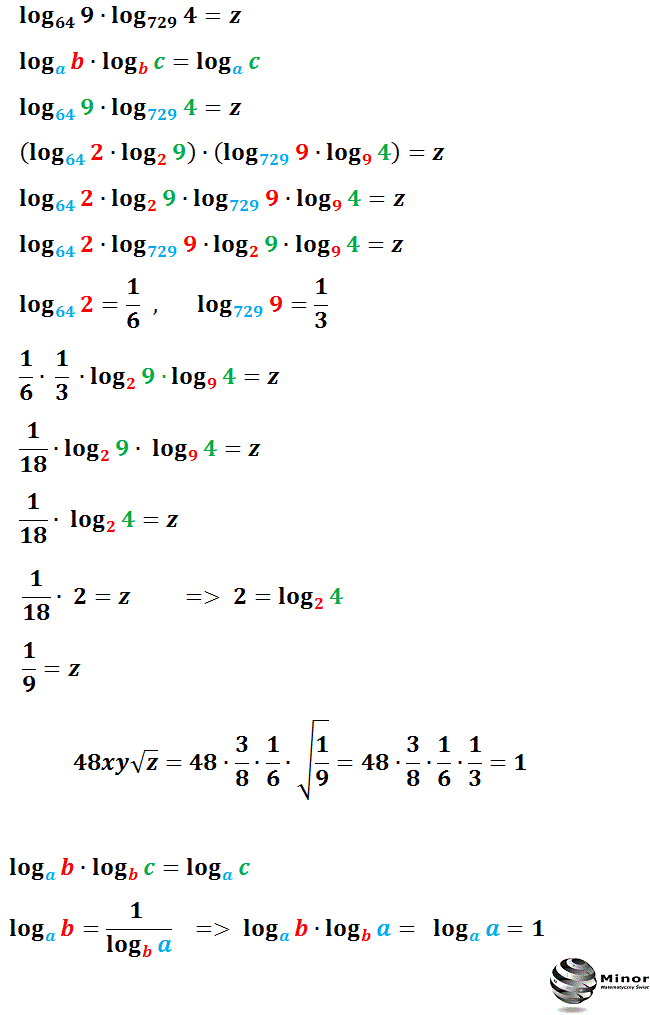
Blog matematyczny Minor Matematyka Mnożenie logarytmów
Definicja logarytmu wygląda tak: W tym wyrażeniu , oraz są liczbami. Zazwyczaj znamy liczby i , a musimy znaleźć liczbę (czyli obliczyć logarytm). W gruncie rzeczy logarytm to po prostu odwrotność potęgowania. Spójrz na przykłady: , ponieważ ; , ponieważ ; , ponieważ .

Mnożenie pierwiastków tych samych stopni YouTube
Wzór na zmianę podstawy logarytmu Stosując następującą metodę możemy zamienić podstawę dowolnego logarytmu: log b ( a) = log x ( a) log x ( b) Uwagi: Nowa podstawa, x , może mieć dowolną wartość. Jak zawsze, aby ten wzór był prawdziwy, argumenty logarytmów muszą być dodatnie a ich podstawy dodatnie i różne od 1 ! Przykład: log 2 ( 50)

Blog matematyczny Minor Matematyka Działania na potęgach
Można to wyrazić za pomocą równania logarytmicznego log 2 ( 16) = 4 , które czytamy jako "logarytm o podstawie dwa z szesnastu równa się cztery". Oba równania wyrażają tę samą zależność pomiędzy liczbami 2 , 4 , oraz 16 , gdzie 2 to podstawa, a 4 to wykładnik. Różnica między potęgą a logarytmem polega na tym, że wynikiem.

Blog matematyczny Minor Matematyka Działania na potęgach
Mamy tu iloczyn potęg o tej samej podstawie, wiec: A=10^6,2+(−4) czyli 10^2,2. Odpowiedz. Ania W końcu ogarnęłam logarytmy : D dzięki! Odpowiedz. Emi_M1 Świetna strona :D. To w sumie wynika wprost z istoty logarytmów, bo jak masz przykładowo log5 z 5^20, to musisz odpowiedzieć sobie na pytanie „do jakiej potęgi trzeba.

Pin on Matematyka
Ucz się z Quizlet i zapamiętaj fiszki zawierające takie pojęcia, jak potęgi - mnożenie, potęgi - dzielenie, potęgi - potęgowanie itp.. logarytm z ilorazu jest równy różnicy logarytmów o tej samej podstawie. logarytm - potęgi. logarytm potęgi jest równy iloczynowi wykładnika tej potęgi i logarytmowi z podstawy. O nas.

Blog matematyczny Minor Matematyka Działania na potęgach
Metoda liczenia logarytmów. Przypuśćmy, że musimy obliczyć loga b. Wynik takiego działania oznaczamy sobie przez x. Zatem mamy: loga b = x. Zgodnie z definicją logarytmu możemy teraz przekształcić to równanie na następujące: ax = b. Teraz z otrzymanego równania wyliczamy liczbę x.

Blog matematyczny Minor Matematyka Mnożenie logarytmów
Zadanie 1 Oblicz: ROZWIĄZANIE:WSKAZÓWKI:1. Skorzystaj ze wzoru na sumę logarytmów o tej samej podstawie. Jeśli dodajemy do siebie dwa logarytmy o tej samej podstawie to w rezultacie…

Ejercicios de unidades de medidas 1a by Gerson Villa Gonzalez Issuu
Jeżeli chcemy odjąć od siebie dwa logarytmy o tej samej podstawie, to możemy skorzystać ze wzoru: logab − logac = loga (b c) l o g a b − l o g a c = l o g a ( b c) Sprawdźmy jak te wzory są wykorzystywane w praktyce: Przykład 1. Oblicz log24 + log22 l o g 2 4 + l o g 2 2.

Mnożenie i dzielenie potęgo tej samej podstawie Brainly.pl
Przykład 1. Oblicz log2 6 +log2 2 3. Rozwiązanie: Korzystamy ze wzoru na dodawanie logarytmów: loga b +loga c = loga(b ⋅ c): log2 6 +log2 2 3 =log2(6 ⋅ 2 3) =log2 4 = 2 Przykład 2. Oblicz log3 18 −log3 2. Rozwiązanie: Korzystamy ze wzoru na odejmowanie logarytmów: loga b −loga c = loga(b c): log3 18 −log3 2 = log3(18 2) = log3 9 = 2 Przykład 3.

19. Dodawanie logarytmów o tej samej podstawie YouTube
Wyzwanie Sprawdź swoje umiejętności w zakresie objętym tą ścieżką. Zacznij wyzwanie z kursu Matematyka Algebra 2 Część 8: Logarytmy Do zdobycia jest 900 punktów za mistrzostwo Opanowane Biegły Zaznajomiony Podjęto próbę Nierozpoczęte Quiz Test sprawdzający O tym dziale Logarytm jest funkcją odwrotną do funkcji wykładniczej.

Bardzo proszę o pomoc. Pilne. Mnożenie i dzielenie potęg o tej samej
Definicja Logarytmem liczby b przy podstawie a nazywamy taką liczbę c, że a podniesione do potęgi c daje liczbę b. Matematycznie zapiszemy tę definicję tak: loga b = c to ac = b Zatem żeby obliczyć loga b, wystarczy odpowiedzieć na pytanie: Do jakiej potęgi podnieść liczbę a, żeby otrzymać liczbę b?

Mnożenie i dzielenie potęg Zadanie Matfiz24.pl YouTube
Wzór logarytmu wygląda tak: logab = c Wtedy i tylko wtedy, gdy: ac = b Poszczególne litery tego ogólnego wzoru odczytamy następująco: a - podstawa logarytmu b - liczba logarytmowana c - logarytm Logarytm przy podstawie a z liczby b wynosi c.

Blog matematyczny Minor Matematyka Działania na potęgach
Działania na logarytmach - dodawanie logarytmów o tych samych podstawach Jeśli chcemy dodać do siebie logarytmy o tych samych podstawach korzystamy ze wzoru logax +logay =loga(x ⋅y) l o g a x + l o g a y = l o g a ( x ⋅ y) Przykłady: Przedstaw logarytm w prostszej postaci.