Amour d'Enfants et IEF Cube du Binôme et les identités remarquables

Pin by mallouka on Matemática Básica E.F Math lessons, Learning mathematics, Education math

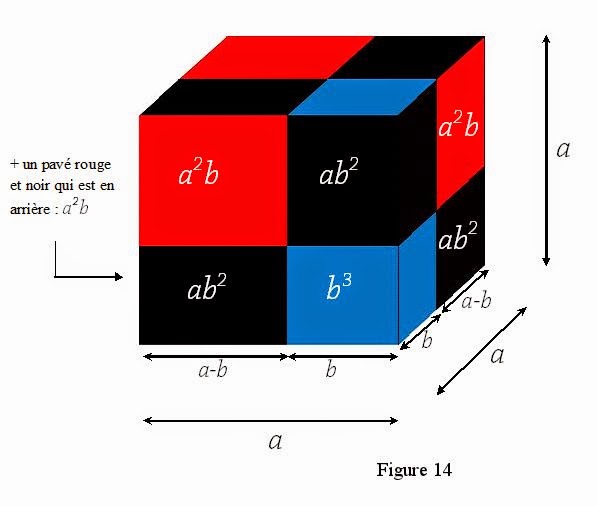
Pour calculer la première identité remarquable, on n'a pas eu besoin de plus de quatre pièces du cube du trinôme. Et si on jouait à faire des maths beaucoup plus avancées de manière aussi simple ? Utilisation du cube du binôme pour calculer les volumes Pour calculer géométriquement (a + b)^3 Cette fois ci, on va passer en 3D.

Amour d'Enfants et IEF Cube du Binôme et les identités remarquables

Nombres, curiosités, théorie et usages: tableau donnant toutes les identités remarquables, curiosités, références - démonstration visuelle ou muette

identite remarquable au cube

2 - Les identités remarquables. En quatrième, nous avons vu comment développer une expression littérale en utilisant la distributivité a× (b+c)=a×b+a×c et la double distributivité (a+b)× (c+d)=a×c+a×d+b×c+b×d. Dans ce cours, nous allons voir trois égalités qui permettent d'aller plus vite quand on fait du calcul littéral.

PDF Télécharger IDENTITES REMARQUABLES Gratuit PDF

Factorisation grâce aux identités remarquables Factorisation de la somme de deux cubes À propos Transcription L'identité a^3 + b^3 = (a + b) (a² - ab + b²). Créés par Sal Khan et Monterey Institute for Technology and Education. Questions Conseils et remerciements Vous souhaitez rejoindre la discussion ? Connectez-vous Trier par :

Mise à jour 85+ imagen formule identité remarquable 3eme fr.thptnganamst.edu.vn

Les identités remarquables sont des égalités qui permettent de développer ou de factoriser facilement une expression.

Cube du binôme.pdf Cubes, Identités remarquables, Jeunes enfants

Leçon 10: Les identités remarquables. Carré d'un binôme. Identifier un trinôme carré d'une somme. Développer un produit de la forme (x + a) (x - a) Développer (a+b) (a-b) Factoriser une différence de deux carrés. Les identités remarquables. Factoriser une différence de deux carrés. Factoriser une différence de deux carrés.

Identités remarquables Corrigé série d'exercices 1 AlloSchool

Les identités remarquables (3e) Elles sont très utiles pour développer ou factoriser des expressions littérales rapidement. Il faut les connaître dans les 2 sens . 1) Carré d'une somme. (a+b)² = a² + 2 × a × b + b² ; noté aussi : (a+b)² = a² + 2ab + b². a² + b² : somme des carrés. 2 × a × b ou 2ab : double produit. Exemples.

Identité remarquable au cube TCT Korea

Les identités remarquables sont au nombre de 3 et sont à apprendre PAR COEUR !!!!! — Remarque importante : on peut inverser (a + b) et (a - b) dans la troisième formule, cela n'a aucune importance. La dernière formule peut donc également s'écrire (a - b) (a + b) = a 2 - b 2 —

Calcul des identités remarquables avec le cube du trinôme Montessori Bout de chou en éveil

Identité remarquable du cube (3D virtuelle) Auteur : Philippe Ligarius (LPH) Thème : Cube Identité remarquable du cube tronqué : Modifier les dimensions des cubes intérieur ou extérieur Déterminer les volumes de chaque cube Vérifier l'identité remarquable sur les volumes

Identité Remarquable (programme mViewer GX Creator Lua Nspire)

HOUSTON, TEXAS - JUNE 14, 2021 - Nanoracks successfully completed the 20 th CubeSat deployment mission from the Company's commercially developed platform on the International Space Station (ISS). Having released two CubeSats into low-Earth orbit, this mission marks Nanoracks' 262nd CubeSat released from the ISS, and the 285th small satellite deployed by Nanoracks overall.

Découvrir 111+ imagen identité remarquable formule générale fr.thptnganamst.edu.vn

Le volume du grand cube, de coté a, est la somme des volumes de trois parallélépipèdes dont un des cotés vaut a-b et d'un cube de coté b (absent ci-contre). a2 + b2 = [(a+b)2 + (a-b)2] / 2 En rose et vert il apparaît deux fois a2 + b2, dont l'aire est celle du plus grand carré, de coté a+b augmentée de celle du plus petit, de coté a.

Calcul des identités remarquables avec le cube du trinôme Montessori Bout de chou en éveil

Cette équation a deux solutions. et 2 S = { − ; } 1 − 2. Exemple 4: Résoudre l'équation : 2 + 2 + 1 − ( + 1)(5 + 4) = 0 Cette équation n'a pas de facteur commun et n'est pas une identité remarquable. Or 2 + 2 + 1 est une identité remarquable, on la factorise : 2 + 2 + 1 = ( + 1)2 On remplace dans l'expression la partie.

Identité remarquable au cube TCT Korea

Retrouvez le cours complet sur les identités remarquables sur Mathsbook : http://www.mathsbook.fr/cours-maths-identites-remarquables-3-479Dans cette vidéo de.

LES IDENTITES REMARQUABLES EXERCICES RESOLUS YouTube

Identités remarquables. Propriété 1 : On considère deux nombres quelconques a et b. ( a + b) 2 = a 2 + 2 a b + b 2. ( a − b) 2 = a 2 − 2 a b + b 2. ( a − b) ( a + b) = a 2 − b 2. Remarque : Cette propriété s'utilise aussi bien pour développer une expression que pour la factoriser.

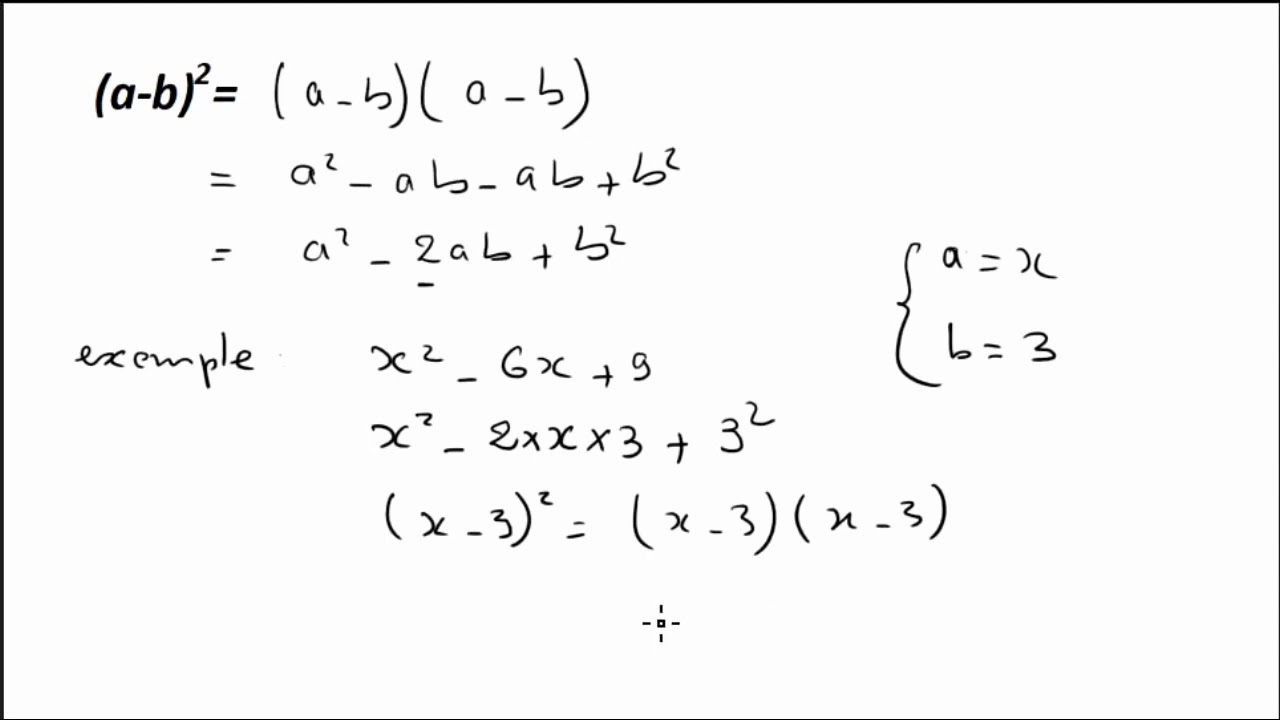
les identités remarquables au carré et au cube YouTube

Algèbre - Identités remarquables 1. Propriétés des opérations 2. Identités remarquables 3. Fractions 4. Puissances 5. Racines carrés et racines -ièmes 6. Polynômes 7. Méthodes de factorisation 8. Résolution d'équations 2e degré Carré d'une somme : $ {\left ( {a + b} \right)^2} = {a^2} + 2ab + {b^2}$

Montessori Equation Cards for Binomial and Trinomial Cube Mathematics, Montessori, Cube

pour comprendre cette identité remarquable, on peut construire un cube de côté (a + b) et exprimer de deux façons le volume du cube : a 3 - b 3 = (a - b) ( a² + ab +b²) a 3 + b 3 = (a + b) ( a² - ab +b²) Exemples d'application pour développer ou factoriser Utiliser la calculatrice des polynômes pour vérifier vos calculs.