Vektor berechnen • Verbindungsvektor zwischen zwei Punkten · [mit Video]

Vektor zwischen zwei Punkten bestimmen, Verbindungsvektor Verständlich erklärt YouTube

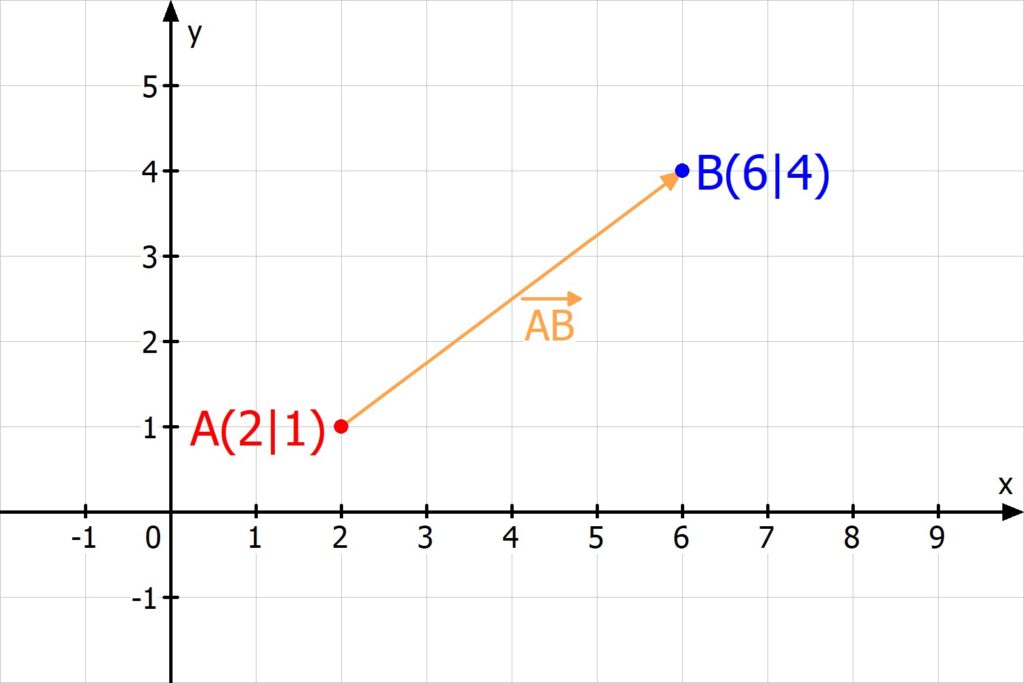
Um den Vektor zu berechnen, der die Punkte A und B verbindet, musst du A von B abziehen. Der Verbindungsvektor beginnt dann bei A (Fußpunkt) und endet bei B (Spitze) . Beispiel: Der Vektor zwischen zwei Punkten A (2|1) und B (6|4) ist. Auch im Dreidimensionalen kannst du einen Vektor aus zwei Punkten bestimmen.

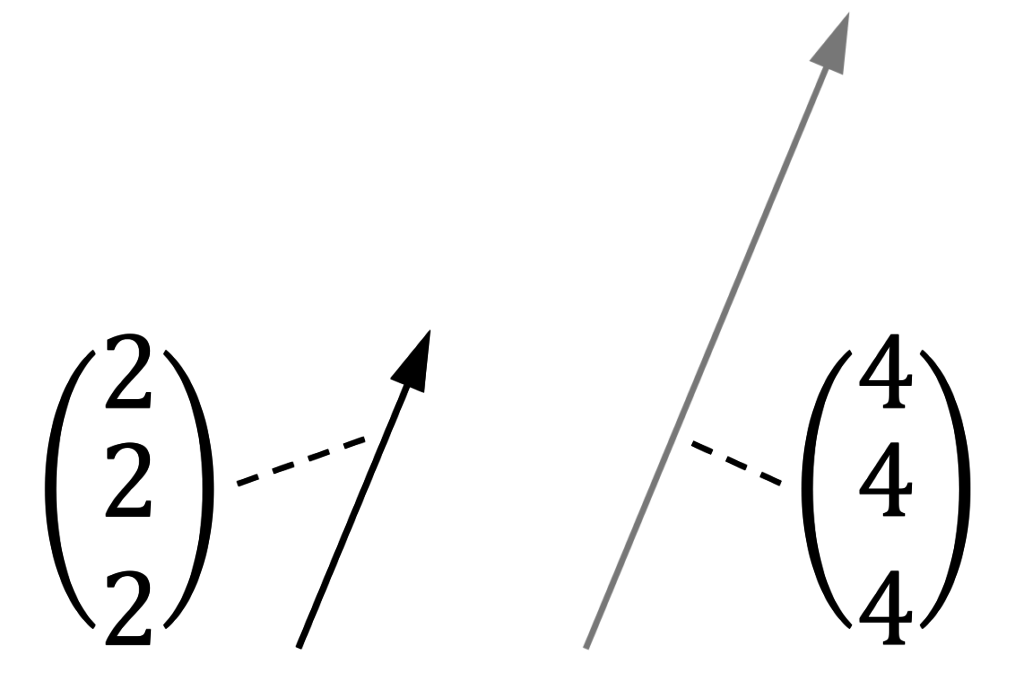
Vektor Zwischen Zwei Punkten Berechnen

Der Verbindungsvektor zwischen zwei Punkten und ist: Die Länge eines Vektors berechnet man wie folgt: Um den Abstand der Punkte und zu bestimmen, wird zunächst der Verbindungsvektor zwischen diesen Punkten aufgestellt: Der Abstand zwischen und entspricht der Länge des Vektors und berechnet sich wie folgt: Ein Skalar ist eine reelle Zahl.

Vektor aus zwei PunktenOrtsvektor YouTube

Allerdings sind Vektoren oft nur dadurch gegeben, dass die Koordinaten zweier Punkte (z.B. A A A und B B B genannt) angegeben werden, zwischen denen ein Repräsentant des Vektors verläuft. In diesem Fall bezeichnet man den Vektor v ⃗ \vec{v} v auch mit A B → \overrightarrow{AB} A B .

Vektorrechnung Geradengleichung mit zwei Punkten bestimmen YouTube

Verbindungsvektor berechnen. Möchtet ihr den Verbindungsvektor zweier Punkte wissen, müsst ihr dazu nur die Koordinaten (bzw die Vektoren der Punkte) voneinander Abziehen mit der Regel "Spitze minus Fuß". Das bedeutet, ihr zieht den Punkt, an dem der Vektor beginnen soll, von dem Punkt ab, an dem der Vektor enden soll. Das sieht wie folgt aus:

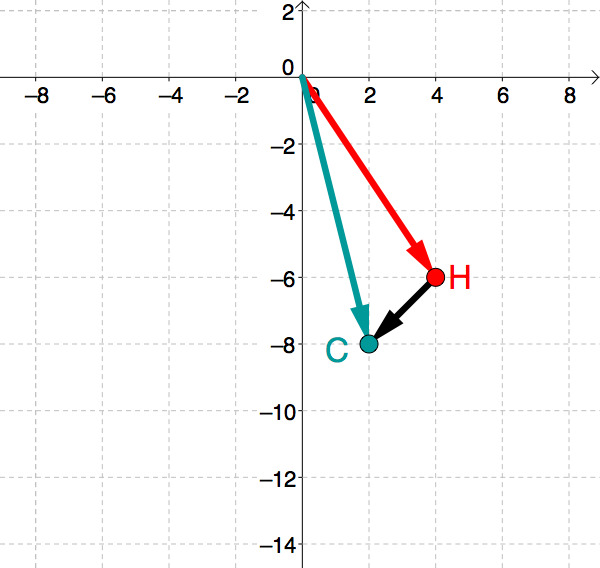
Vektor zwischen zwei Punkten berechnen lernen mit Serlo!

Berechne den Verbindungsvektor \overrightarrow {\text {PQ}} PQ der Punkte \text P (1;3) P(1;3) und \text Q (3;2) Q(3;2). Der Verbindungsvektor  \overrightarrow {\text {PQ}} PQ wird als Differenzvektor berechnet. Dabei gilt die Regel: Vorgehen. "Spitze minus Fuß".

Vektorrechnung im Abi 2022 Verbindungsvektor zwischen zwei Punkten aufstellen YouTube

Ein Vektor ist die kürzeste Verbindung zwischen zwei Punkten. In diesem Fall ist das ein Vektor zwischen einem Haus (= Koordinatenursprung) und einem Schatz. Einen Vektor kannst du dir wie eine Wegbeschreibung in 3D vorstellen. Den Vektor, den du in der Animation sehen kannst, würdest du folgendermaßen aufschreiben.

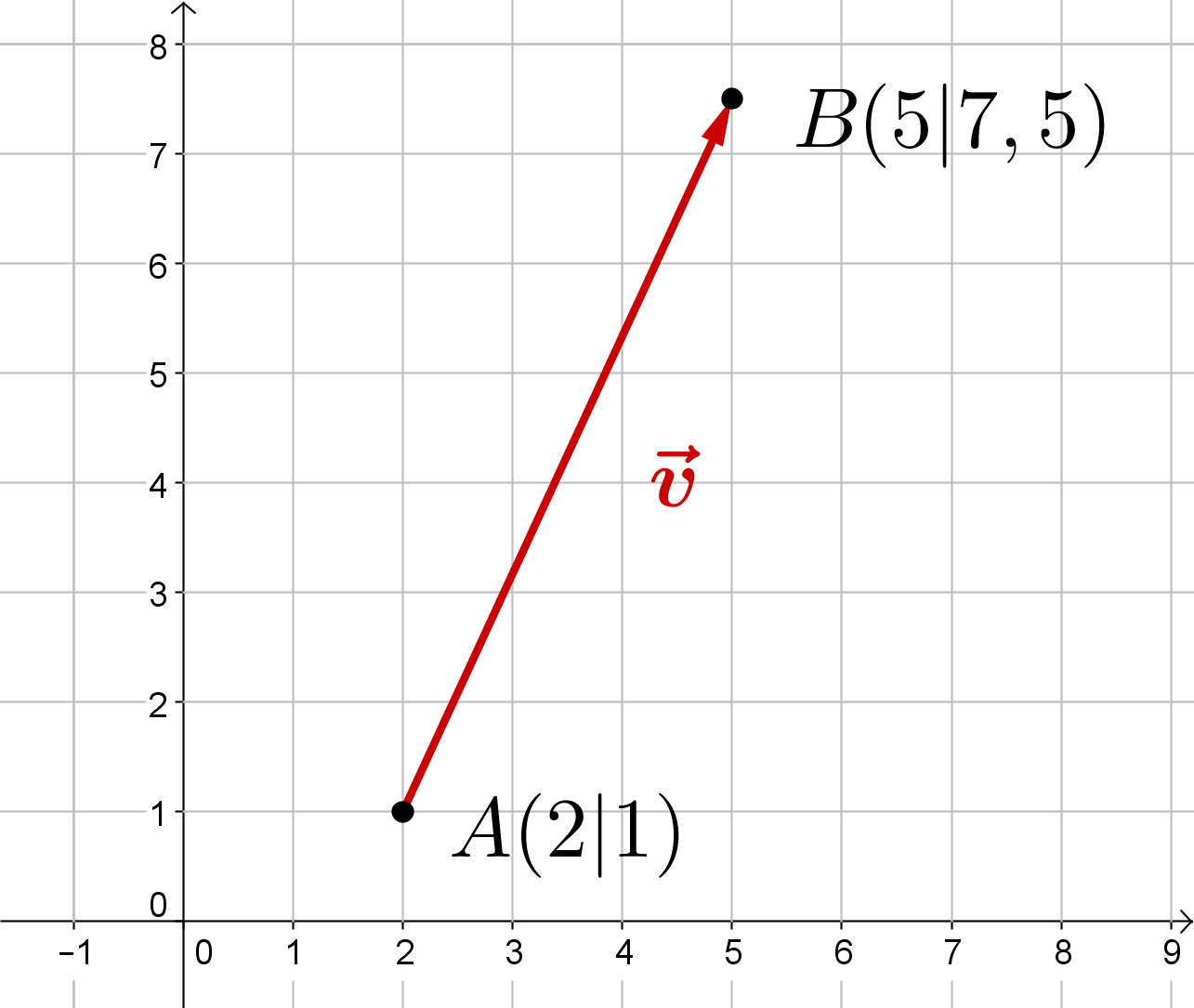
Aufgaben zur Berechnung eines Vektors zwischen zwei Punkten lernen mit Serlo!

Aufgaben zur Berechnung eines Vektors zwischen zwei Punkten Hier findest du Aufgaben zur Berechnung eines Vektors zwischen zwei Punkten. Übe dabei sowohl im zwei- als auch im dreidimensionalen Koordinatensystem. 1 Vektor gesucht Bestimme den Vektor, indem du die richtigen Koordinaten zuordnest. Überprüfen Rights of use Lösung anzeigen 2

Vektorrechnung Abstand zwischen zwei Punkten Betrag eines Vektors Länge eines Vektors YouTube

Du kannst mit der Subtraktion von zwei Punkten A und B den Vektor ausrechnen, der A und B verbindet. Das ist der Verbindungsvektor. Also ist der Verbindungsvektor zwischen A = (2 | 8 | 5) und B = (1 | 4 | 3): Der Abstand zwischen A und B ist die Länge des Verbindungsvektors . In unserem Beispiel ist der Abstand zwischen A und B also:

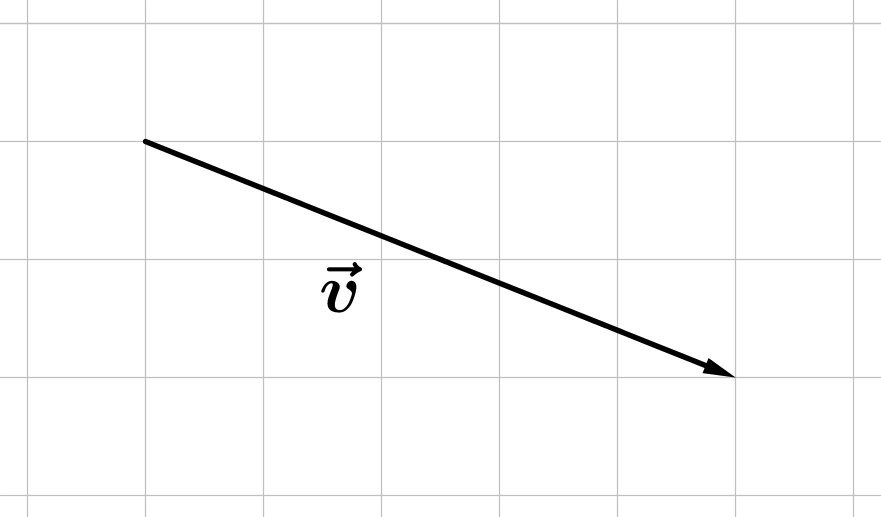
Aufgaben zur Berechnung eines Vektors zwischen zwei Punkten lernen mit Serlo!

Vektor zwischen zwei Punkten Beispiel Von Punkt P (3|1|4) zu Punkt Q (4|4|3). In x 1 -Richtung: von 3 zu 4 entspricht 4-3=1 (1 nach vorne). In x 2 -Richtung: von 1 zu 4 entspricht 4-1=3 (3 nach rechts) und in x 3 -Richtung: von 4 zu 3 entspricht 3-4=-1 (1 nach unten).

Bestimmung eines Vektors zwischen 2 Punkten von Marco Bakera YouTube

Mit meinem Online-Rechner kannst du ganz einfach den Verbindungsvektor zweier Punkte berechnen. Inhaltsverzeichnis Eingabe Ausgabe Beispiel Verwandte Online-Rechner Erforderliches Vorwissen Verbindungsvektor Im Folgenden erkläre ich dir kurz, wie der Rechner funktioniert.

Vektoren Abstand von zwei Punkten berechnen by einfach mathe! YouTube

Lineare Abhängigkeit 2 Vektoren: Wann sind zwei Vektoren linear abhängig? Lineare Abhängigkeit 3 Vektoren: Wann sind drei Vektoren linear abhängig? Lineare Unabhängigkeit: Wie kann man mithilfe der Determinante feststellen, ob Vektoren linear unabhängig sind? Anwendungen: Abstand zweier Punkte: Wie berechnet man den Abstand zwischen zwei.

Vektorrechnung in R2 10 Normalvektor und Mittelpunkt zwischen 2 Punkten YouTube

Um den gesuchten Vektor zu erhalten, braucht man zuerst lediglich die beiden Ortsvektoren zu Punkt A und Punkt B. Dann zieht man den Vektor zu Punkt B vom Vektor zu Punkt A ab - und man erhält den neuen Vektor von A nach B. Wiederholung: Ortsvektor

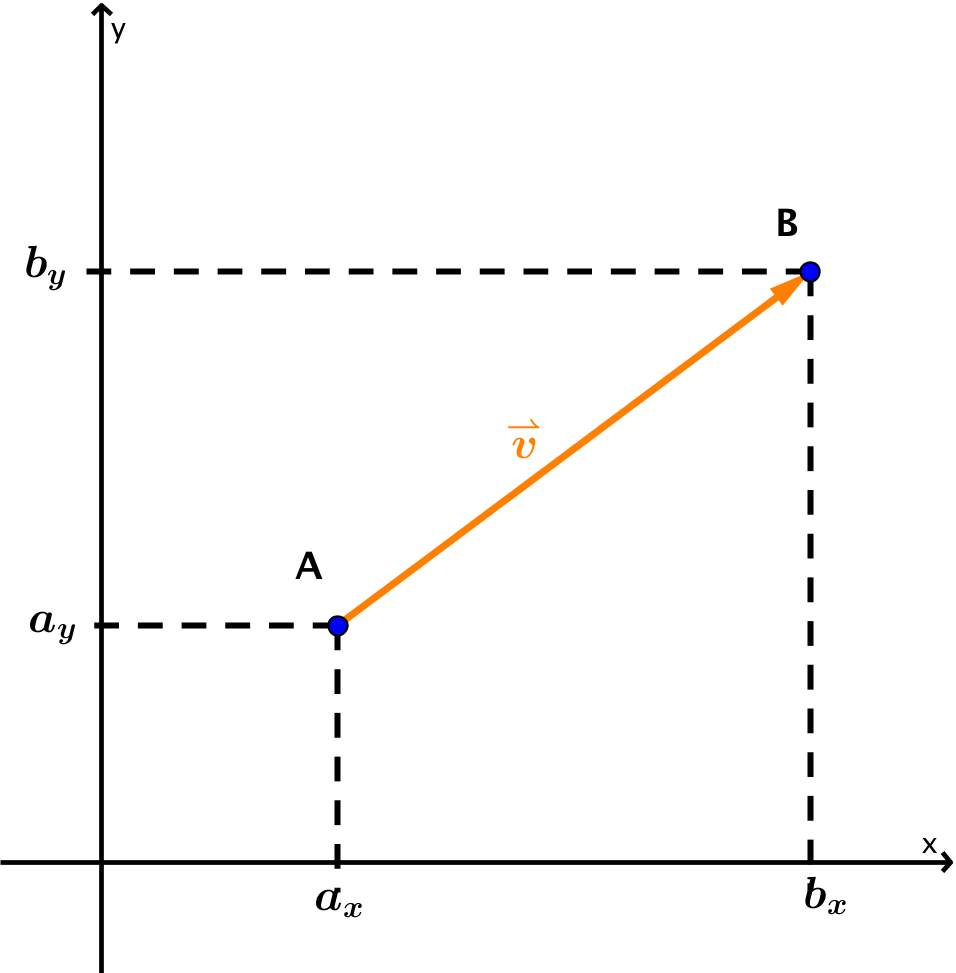
Einführung in den Vektorbegriff (Vektoren in der Ebene I) Aufstellen des Vektors zwischen zwei

Vektor zwischen zwei Punkten berechnen Um den Verbindungsvektor zwischen zwei Punkten A und B zu berechnen, muss man den Ortsvektor zu Punkt A vom Ortsvektor zu Punkt B subtrahieren. Merke "Spitze minus Fuß" Im Zweidimensionalen: A\left (a_1|a_2\right),\;B\left (b_1|b_2\right) A(a1∣a2), B(b1∣b2)

Vektorrechnung in R2 04 Betrag, Einheitsvektor, Vektor zwischen zwei Punkten YouTube

(00:49) Vektoren durch zwei Punkte berechnen (02:48) Vektoren addieren und subtrahieren (02:00) Skalarmultiplikation (03:44) In diesem Beitrag erklären wir dir, was ein Vektor ist und was du mit ihm beschreiben kannst. Du möchtest in kurzer Zeit alles Wichtige zum Thema Vektor erfahren? Dann schau dir unser Video dazu an! Inhaltsübersicht

Vektor und Gegenvektor zwischen zwei Punkten bestimmen YouTube

Zwei Punkte im Raum können ident bzw. deckungsgleich sein, oder sie können einen Abstand von einander haben. Wenn sie nicht ident sind, kann man sie durch eine Gerade verbinden. Die Strecke PQ auf der Geraden g ist der kürzeste Abstand zwischen den beiden Punkten. { P, Q, R } ∈ g d ( P, R) = | P R → | = 0 d ( P, Q) = | P Q → | ≠ 0.

Vektor berechnen • Verbindungsvektor zwischen zwei Punkten · [mit Video]

Vorgehensweise Um den Verbindungsvektor zwischen zwei Punkten A und B zu berechnen muss man den Ortsvektor \vec a a vom Ortsvektor \vec b b subtrahieren. Man schreibt \overrightarrow {AB}=\vec b-\vec a AB = b − a. Dabei hat der Verbindungsvektor die Spitze im Minuend und den Fuß im Subtrahend. Als Merksatz gilt also Spitze minus Fuß. Zurück Weiter