Übungsblatt zu Quadratische Funktionen

Klassenarbeit zu Quadratische Funktionen

dba32ccf7.pdf Um sicher mit quadratischen Funktionen umgehen zu können, braucht man entscheidendes Handwerkszeug: Man muss quadratische Gleichungen lösen können. Übersicht quadratische Gleichungen Check, ob du eine quadratische Gleichung mit Hilfe der quadratischen Ergänzung lösen kannst: hier Check, ob du quadratische Gleichungen durch Ausklammern lösen kannst: hier Nicht das einzige.

Hinweise zum Arbeitsblatt Quadratische Funktionen "Prototyp" und "Verwandte" Zielgruppe

Quadratische Gleichungen lösen. Thema Quadratische Funktionen - Kostenlose Klassenarbeiten und Übungsblätter als PDF-Datei. Kostenlos. Mit Musterlösung. Echte Prüfungsaufgaben.

Nullstellen bei gemischt quadratischen Funktionen YouTube

Quadratische Funktionen einfach erklärt Aufgaben mit Lösungen Zusammenfassung als PDF Jetzt kostenlos dieses Thema lernen!

Arbeitsblatt Die quadratische Funktion Mathematik tutory.de

sind notwendig oder sehr nützlich, da es auch im Thema „Quadratische Funktionen" (QF) immer wieder um lineare Funktionen geht. Außerdem kann man zwischen diesen beiden Funktionsarten Verknüpfungenerstellen,davielesähnlichist. • Was ist eine Funktion? EineFunktiongibtmirzueinemx-Werteineny-Wert.ZumBeispielsagstdumirdenWert x = 5.

Quadratische Funktionen Aufgaben

Quadratische Gleichungen und Funktionen Stand: 25.11.2023 19 Lösungen Grundkompetenzen Lösungserwartung: Gleichung einer quadratischen Funktion* - 1_341, FA3.3, 2 aus 5 Lösungserwartung: Quadratische Funktion* - 1_367, FA3.3, 2 aus 5 Lösungserwartung: Schnittpunkte* - 1_597, FA3.3, 2 aus 5

Quadratische Funktionen

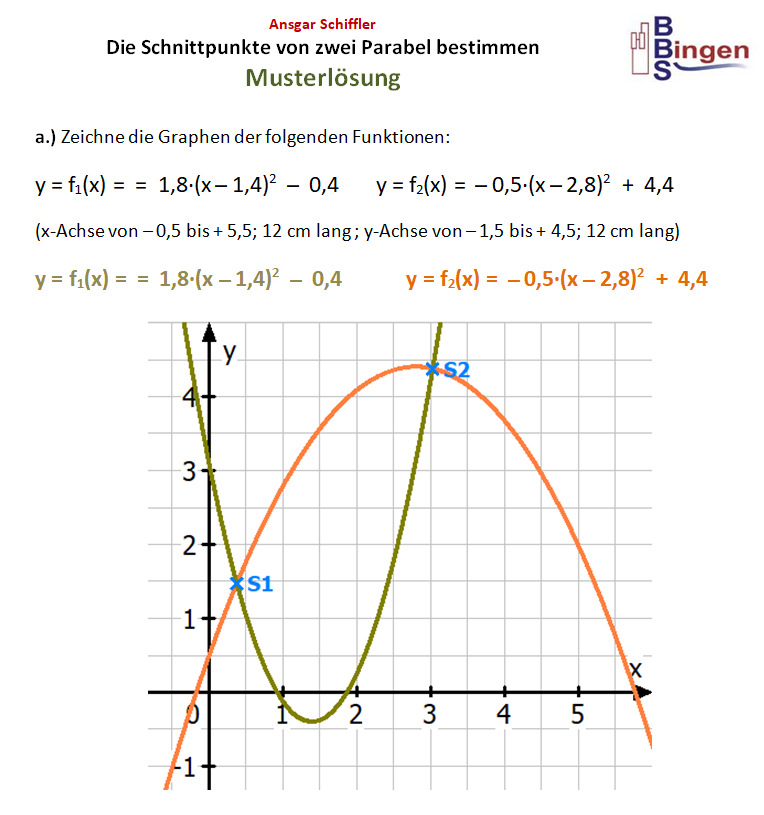
Aufgaben zu quadratischen Funktionen Aufgabe 1: Streckung und Stauchung y 3 Bestimme die Gleichungen der rechts abgebildeten Parabeln: f1(x) = 2 f2(x) = 1 f3(x) = 0 x Zeichne die folgenden Parabeln ebenfalls in das Koordinatensystem: -3 -2 -1 0 1 2 3

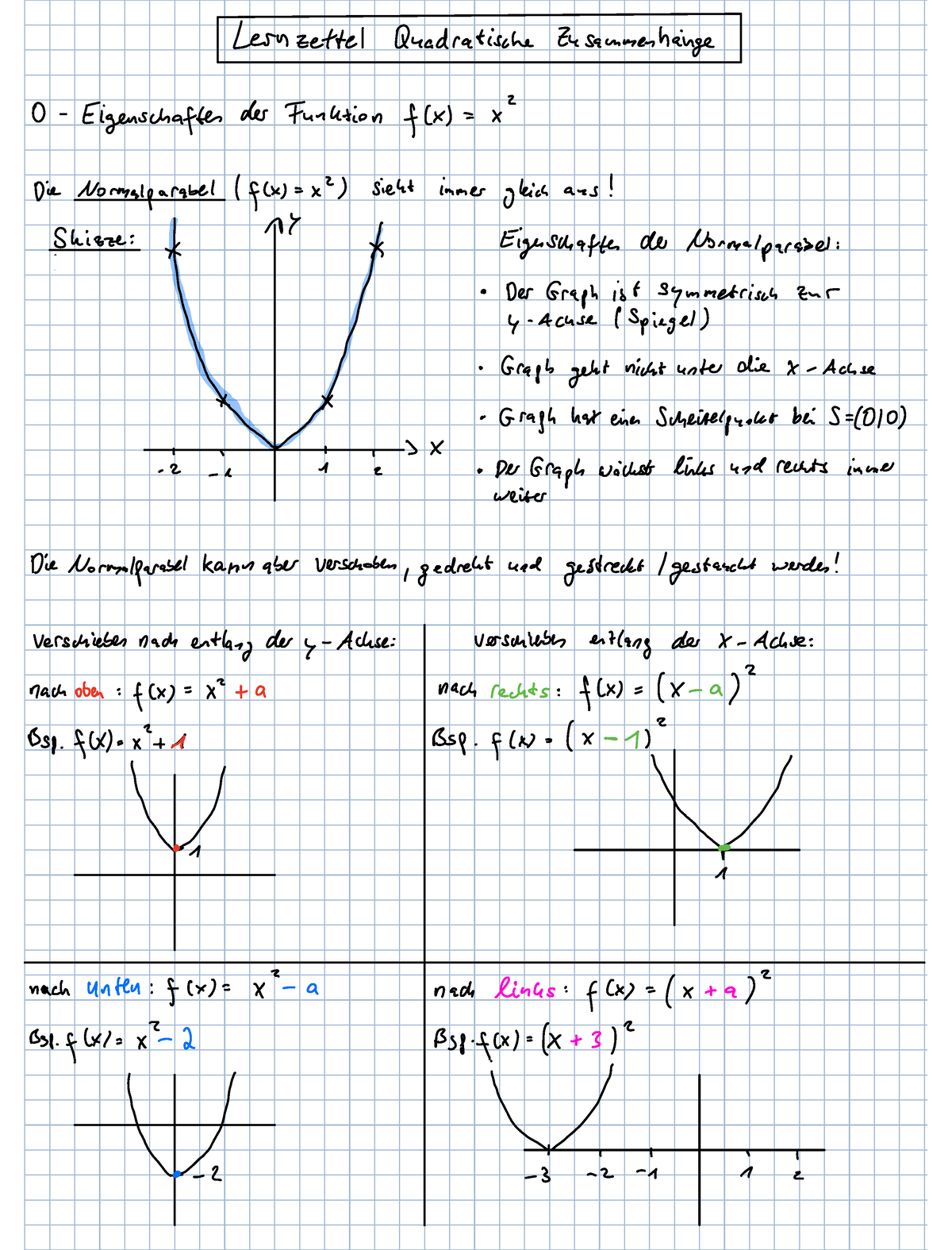
Quadratische Funktion Lernzettel Lernzettel Quadratische Zusammenhänge 0 Eigenschaften der

Wir wollen auf diesem Arbeitsblatt die quadratischen Funktionen (Parabeln) studieren. Wir kennen dabei die folgenden Darstellungsformen: Allgemeine Form: Scheitelpunktform: = ( ) = 2 + + = ( ) = ( − )2 + In der höheren Mathematik werden diese Funktionen als sogenannte „ganzrationale Funktionen" eingeordnet, speziell mit Grad 2.

DateiQuadratische Funktionen.pdf RMGWiki

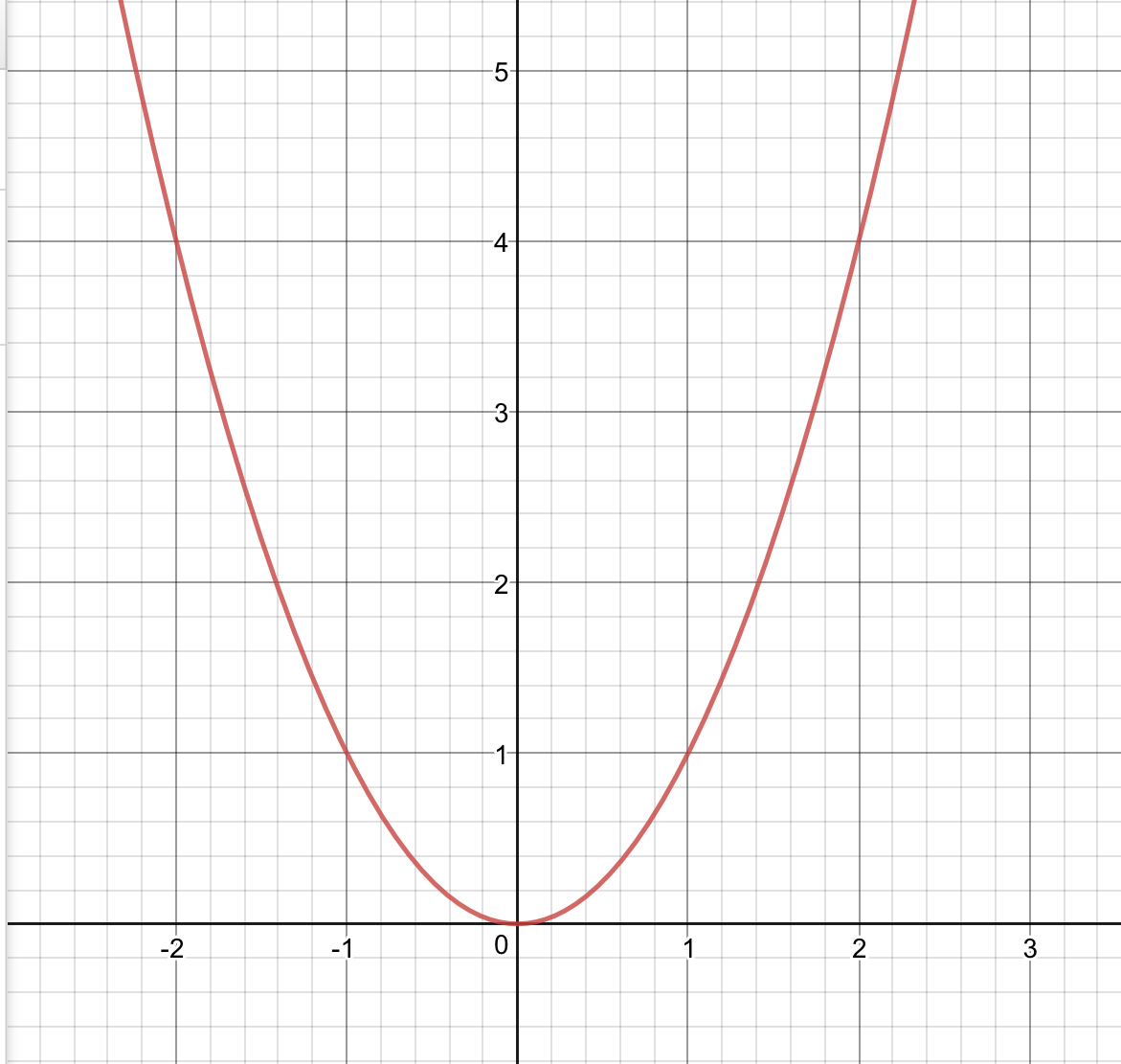
Quadratische Funktionen werden im Allgemeinen durch die Funktionsgleichung f (x) = ax² + bx + c (a, b, c, x ˘ ˇ; a ≠ 0) beschrieben. Der Graph einer quadratischen Funktion ist eine gekrümmte Kurve und heißt Parabel. Die einfachste quadratische Funktion (a = 1, b = c = 0) hat die Funktions gleichung f (x) = x².

Quadratische Gleichungen mit quadratischer Ergänzung lösen Unterrichtsmaterial im Fach

Quadratische Funktionen | Fördern Nullstellen (1) - Lösung 1 S ist der Scheitelpunkt einer nach oben geöffneten, verschobenen Normalparabel. Zeichne die Parabel. Lies dann die Nullstellen ab. a) : F ß | F Ú ; b) : F Ú| Ù ; c) : Ý | Ú ; Ú L F Þ Û L F à L F Ú keine Nullstelle 2 Bestimme den Scheitelpunkt. Zeichne das Schaubild der.

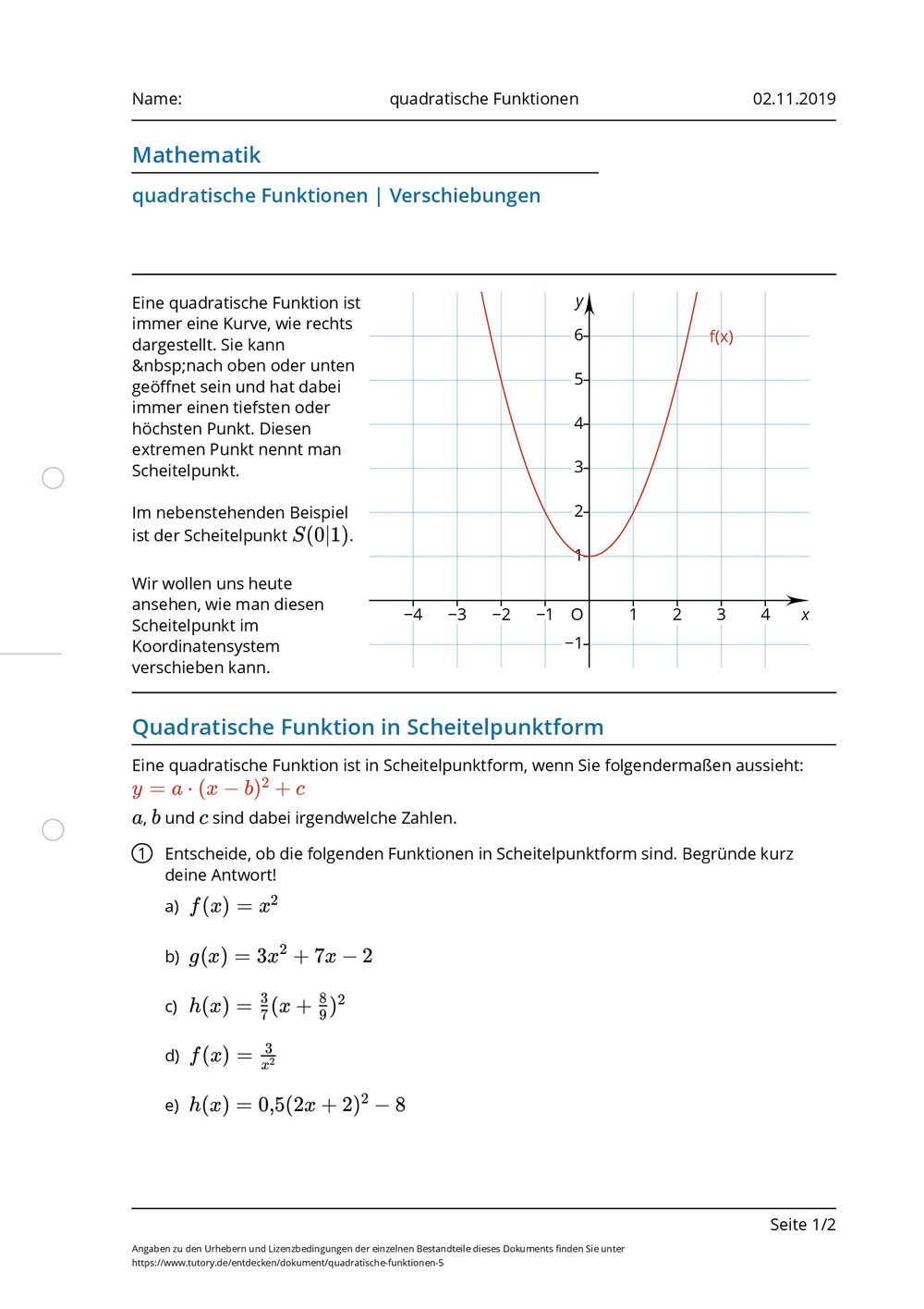
Arbeitsblatt quadratische Funktionen tutory.de

Quadratische Funktionen Übersicht 0. Wiederholung: Lineare Funktionen Normalparabel (Funktion mit der Gleichung y=x2) Gestauchte und gestreckte und gespiegelte Parabeln An den Achsen verschobene Parabeln 3.1 Vertikale Verschiebung 3.2 Horizontale Verschiebung Quadratische Funktionen berechnen (Nullstellen bestimmen)

Übungsblatt zu Quadratische Funktionen

x f (x) 5 4 3 2 1 -1 -2 -3 -4 -5 -6 -7 -8 x y -8 -7 -6 -5 -4 -3 -2 -1 O 1 234567. 2Skizziere die Graphen der folgenden quadratischen Funktionen ohne Wertetabelle. a) f (x) = (x - 3)2- 1 b) f (x) = - (x + 2)2+ 4 c) f (x) = 0,5 (x - 1)2- 2,5 d) f (x) = -2 (x - 1)2+ 2,5.

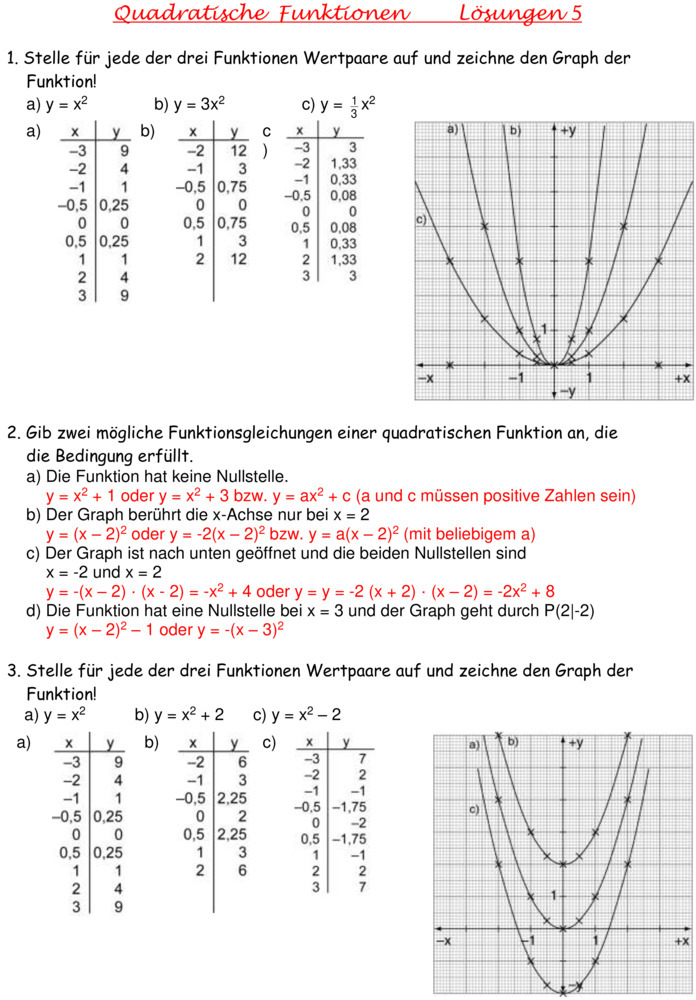
Übungsblatt zu Quadratische Funktionen

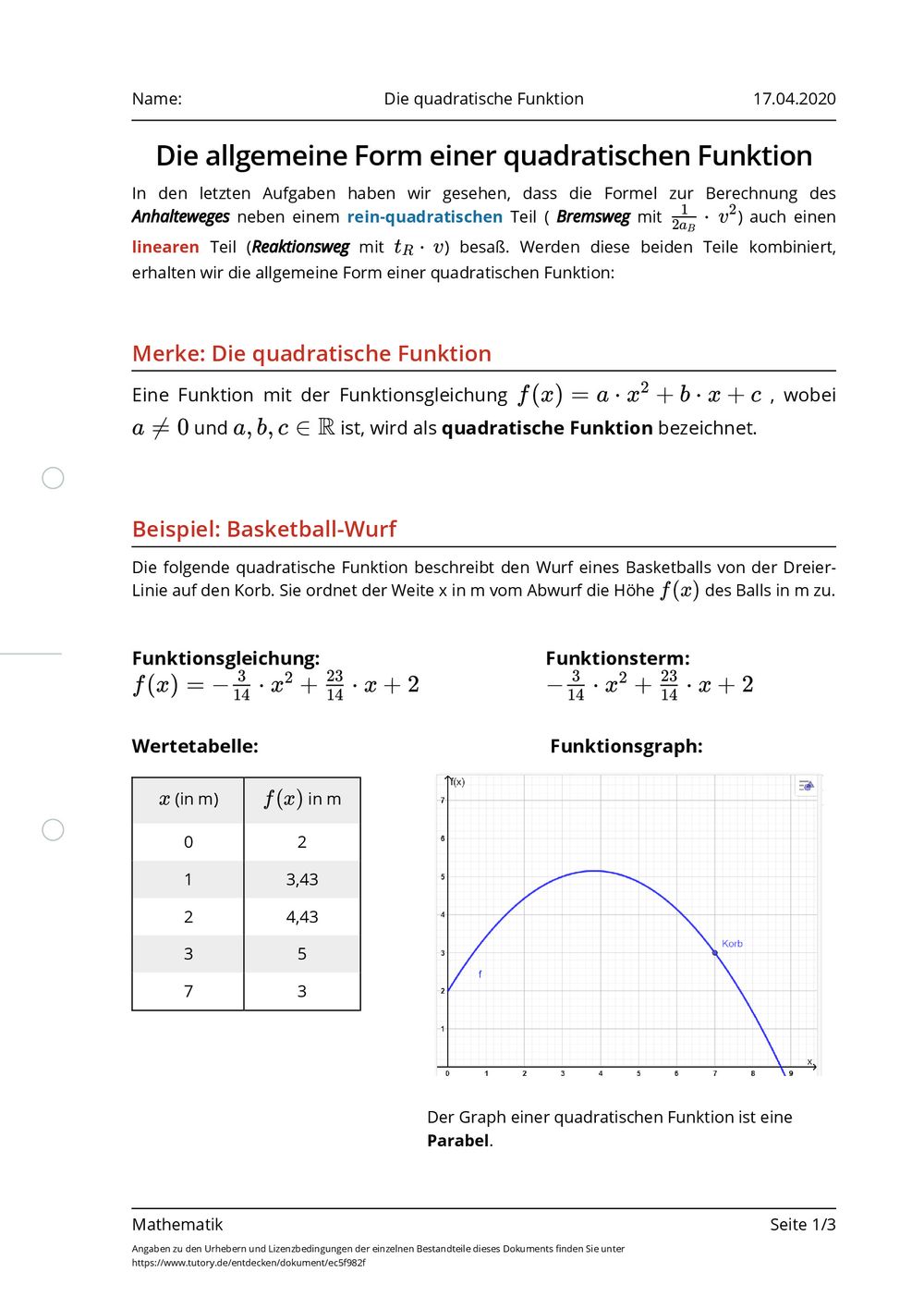
Quadratische Funktionen werden beispielsweise verwendet, um beschleunigte Bewegungen (wie einen Ballwurf) zu beschreiben. Der Graph einer quadratischen Funktion heißt „Parabel". Die Funktion mit der Gleichung ( ) = nennt man Normalparabel. Die allgemeine Funktionsgleichung einer quadratischen Funktion lautet

Übungsblatt zu Quadratische Funktionen

Lösungsblatt: Quadratische Funktionen Version vom 28. April 2020 1 Es gibt zu allen Aufgaben unendlich viele Lösungen. Zur Kontrolle kann bei GeoGebra der Funktionsgraph betrachtet werden. 2 a) f(x) = 1 4 ·(x−1)2 +2 b) f(x) = −1 8 ·(x+2)2 +3 c) f(x) = 4 9 ·(x−4)2 −1 d) f(x) = 1 2 ·x 2 +1 3 a) f(x) = −0,2x2 +0,8x+1 b) f(x) = 0.

Quadratische Funktionen Pdf Quadratische Funktionen Scheitelpunkt Rechner

Quadratische Funktionen haben eine quadrierte Variable (x²). Die einfachste (tschiraquade) Funktion hat die Gleichung y = x². Ihr Graph heißt (paraNormablle). Die Normalparabel verläuft symmetrisch zu der Achse, durch die das (Minumim) verläuft. Sie ist nach (bone) hin geöffnet.

Quadratische Funktionen Übungen und Aufgaben mit Lösungen

f ( x ) = a x 2 + b x + c, wobei a 0. z.B. f ( x ) = -0,5 x 2 + 2 x - 2,5. Der Graph einer quadratischen Funktion heißt quadratische. Parabel. Eigenschaften: positiv (a > 0): Die Parabel fällt zuerst bis zu einer Minimalstelle (der zugehörige Punkt heißt Scheitelpunkt) und steigt danach wieder, linksgekrümmt.

Übungsblatt zu Quadratische Funktionen

Übersicht Quadratische Funktionen Quadratische Funktion erkennen Graph: Parabel Gleichung: Der höchste Exponenti ist 2 Vorsicht: y = x•x ist eine quadratische Funktion, da x•x = x2 Scheitelpunktsform (Lage und Form der Parabel) y = (x + a)2 + b Man kann den Scheitelpunkt der Parabel ablesen. Bsp.: y = (x + 3)2 + 7 Scheitelpunkt: S(-3 / 7)