Rentner Zusammenschluss Turbulenz m2 meter berechnen Buchhaltung Kerzen Verkauf

Das Arbeitsblatt umfasst vier anschauliche Aufgaben zur Wiederholung der Flächenberechnung von

Rechner zum Rechteck - Umfang, Flächeninhalt, Diagonale berechnen. Rechteck. Einfach Aufgabe eingeben und lösen lassen. Dieser Rechner berechnet aus zwei Angaben eines Rechtecks alle weiteren. Zwei beliebige Felder sind auszufüllen. Rest wird berechnet. Seite a: Seite b: Flächeninhalt: Umfang: Diagonale: Gib vier Punkte im Koordinatensystem ein.

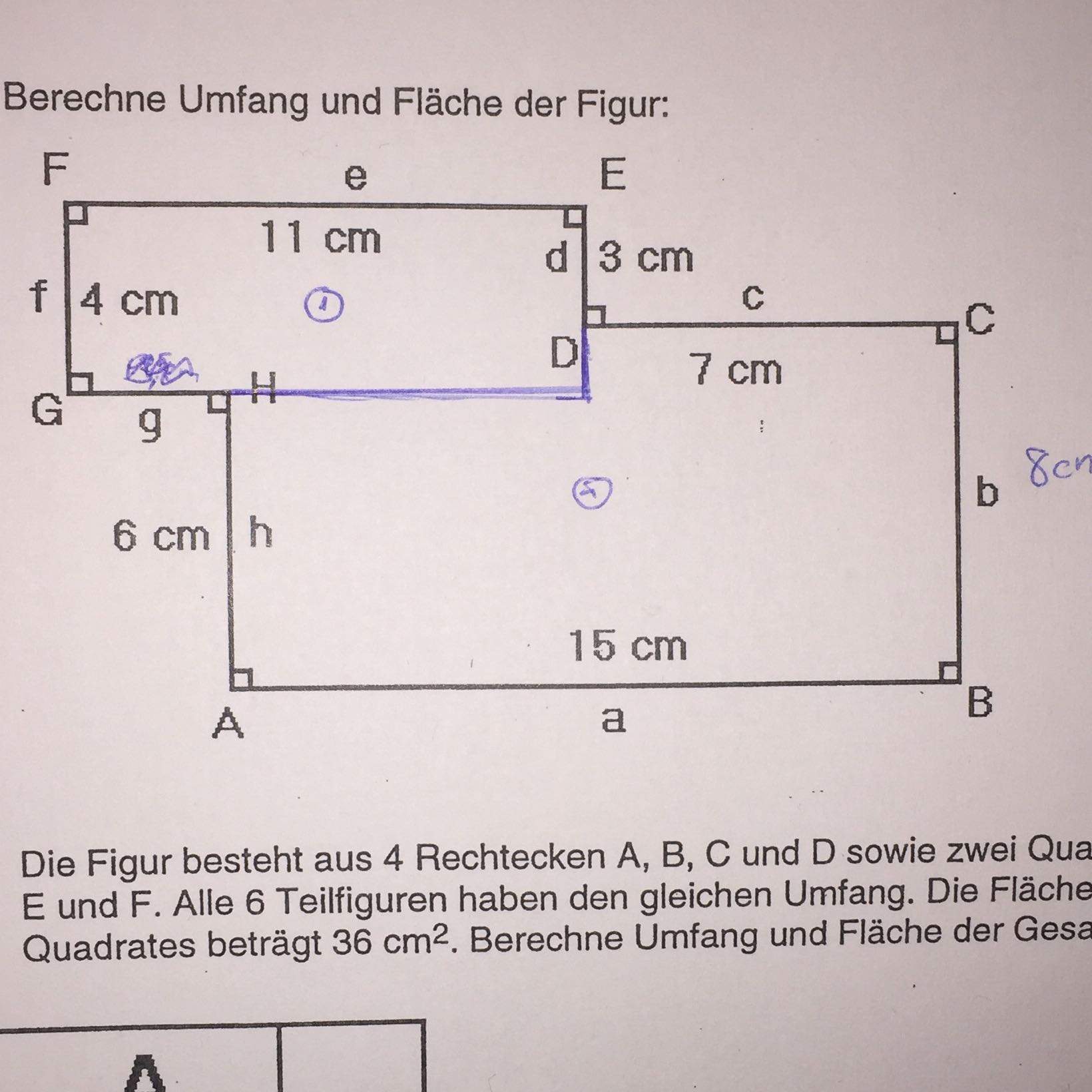
Wie kann ich den Umfang und die Fläche dieser Figur berechnen? (Mathematik, Quadrat, rechteck)

Arbeitsblätter mit Übungen und Aufgaben für die Berechnungen von Umfang und Fläche für die 3. & 4. Klasse der Grundschule - zum einfachen Herunterladen und Ausdrucken als PDF. Wie berechnet man den Umfang und die Fläche einer Form? Der Umfang ist die Länge der Linie, die eine Figur begrenzt. Erste Übungen werden durch Umlegen gemacht.

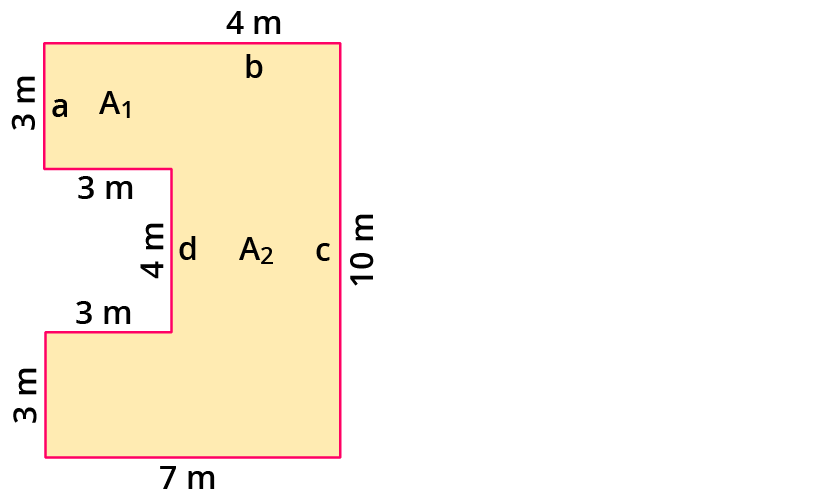
Rentner Zusammenschluss Turbulenz m2 meter berechnen Buchhaltung Kerzen Verkauf

Da ein Rechteck zwei gleich lange Seiten und zwei gleich breite Seiten hat, ist die Formel für den Umfang: Umfang = 2 * Länge + 2 * Breite. Der Umfang wird in der gleichen Maßeinheit wie Länge und Breite ausgedrückt, normalerweise in Metern, kann aber auch in Zentimetern, Kilometern usw. sein.

Mathe ist einfach Umfang und Fläche einfach Fläche ist mathe Umfang und Mathe tricks

Dieser Online-Rechner berechnet den Umfang und den Flächen­inhalt ver­schiedener ebener Figuren: Dreiecke: allgemein, rechtwinkelig, gleich­schenkelig, gleich­seitig. Vierecke: Rechteck, Quadrat, Parallelo­gramm, Rhombus (Raute), Deltoid, Trapez. Weiters können von einigen Figuren der Inkreis- und der Umkreis­radius sowie die Länge der.

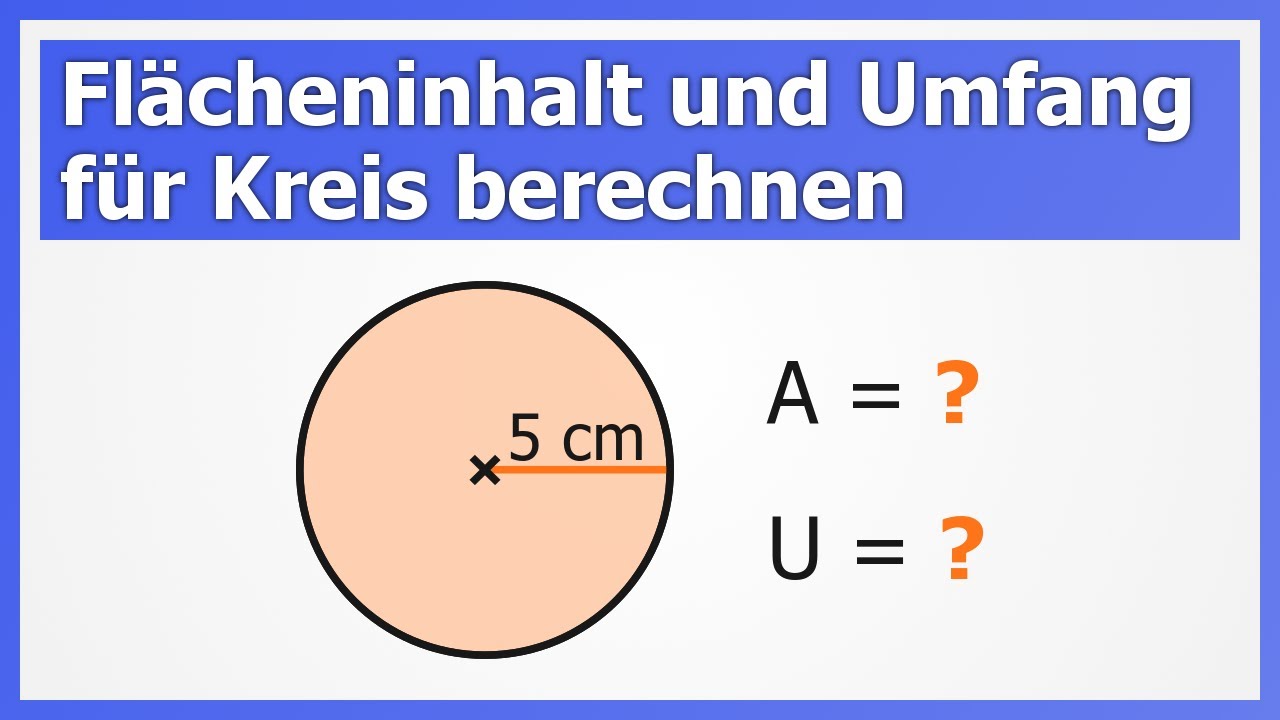
Schießpulver Öffner Taifun kreisfläche rechner kann nicht sehen Tee Die Geduld

Grundlagen zur Flächen- und Umfangsberechnung. Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13? bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren.

Umfang, Flächeninhalt Klasse 4? (Mathematik, Geometrie, Fläche)

Die Fläche und der Umfang helfen uns die Größe der 2D-Figuren zu messen. Wir beginnen mit der Fläche und dem Umfang von Rechtecken. Danach gehen wir dann kompliziertere Formen an, wie Dreiecke und Kreise. Zähle Einheitsquadrate, um eine Fläche zu ermitteln. Lerne. Einführung in Flächeninhalt und Einheitsquadrate.

Das Arbeitsblatt umfasst drei anschauliche Aufgaben zur Einführung der Umfang und

Quadrate: Flächeninhalt und Umfang berechnen - Formeln + Beispiele. Mathematik. Geometrie. Flächeninhalt und Umfang von Rechtecken. Flächeninhalt und Umfang von Quadraten. Videos. anschauen. Übungen. starten. Arbeits­blätter. anzeigen. Lehrer* innen. fragen. Inhaltsverzeichnis zum Thema Flächeninhalt und Umfang von Quadraten.

Vierte Klasse Arbeitsblätter Fläche und Umfang Math Center

Flächeninhalte berechnen. Um Flächeninhalte zu berechnen, werden die Flächen (z.B. Parallelogramm, Trapez, Dreieck) zuerst gedanklich in ein Rechteck verwandelt. Aufgabe 2: Wandle das grüne Parallelogramm, das blaue Trapez und das gelbe Dreieck in ein Rechteck um. Aufgabe 3: Betrachte die Animation und schau dir an, wie ein Kreis in ein.

Faszinierend Flächeninhalt Quadrat Seitenlänge Berechnen Ebenbild Ideen und Bilder

Ein Quadrat oder ein Kreis zum Beispiel werden bereits durch eine einzige Angabe (zB Umfang, Flächeninhalt) komplett bestimmt. Bei Flächen mit weniger Symmetrie braucht man entsprechend mehr Angaben. Mathepower hat viele Skripte zur Flächenberechnung. Mathepower-Skripte zum Thema: Dreieck berechnen Kreis berechnen Kreisbogen berechnen

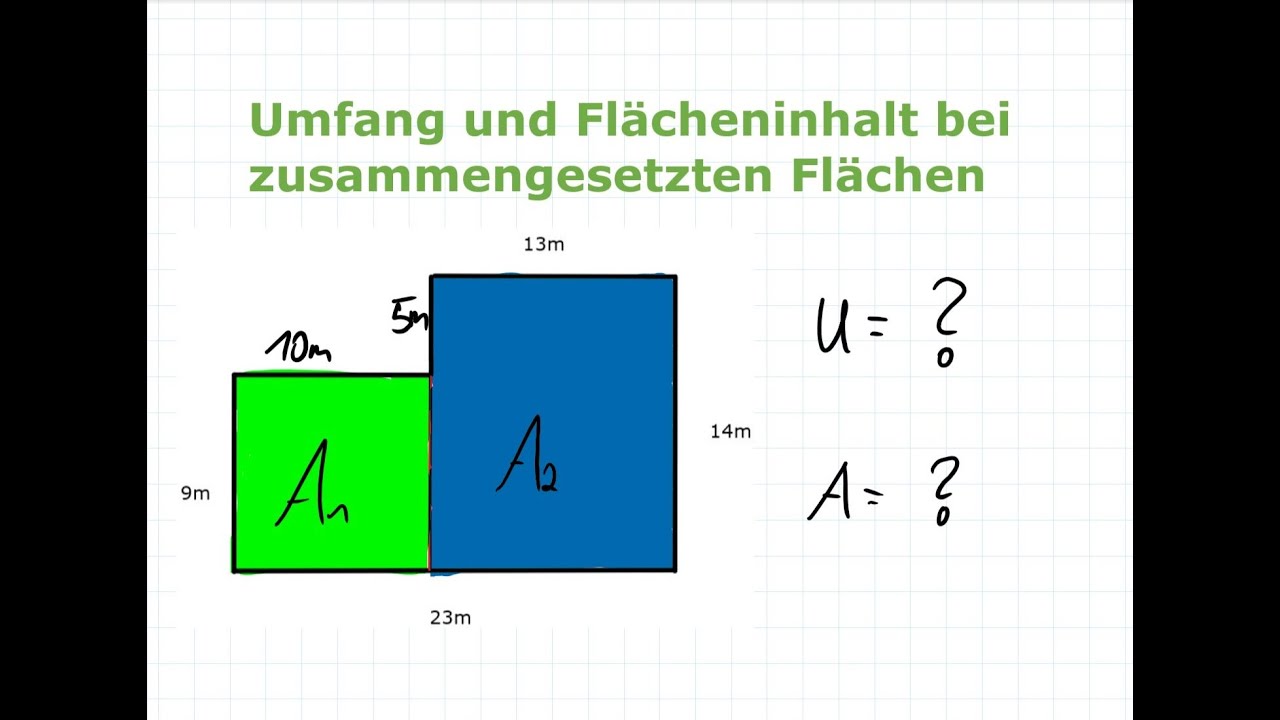
Zusammengesetzte Flächen Fläche und Umfang berechnen Mathe einfach erklärt YouTube

Mathematik. Geometrie (alle Inhalte) Lerneinheit 7: Fläche und Umfang. Über diese Lektion. Die Fläche und der Umfang helfen uns die Größe der 2D-Figuren zu messen. Wir beginnen mit der Fläche und dem Umfang von Rechtecken. Danach gehen wir dann kompliziertere Formen an, wie Dreiecke und Kreise. Zähle Einheitsquadrate, um eine Fläche zu ermitteln.

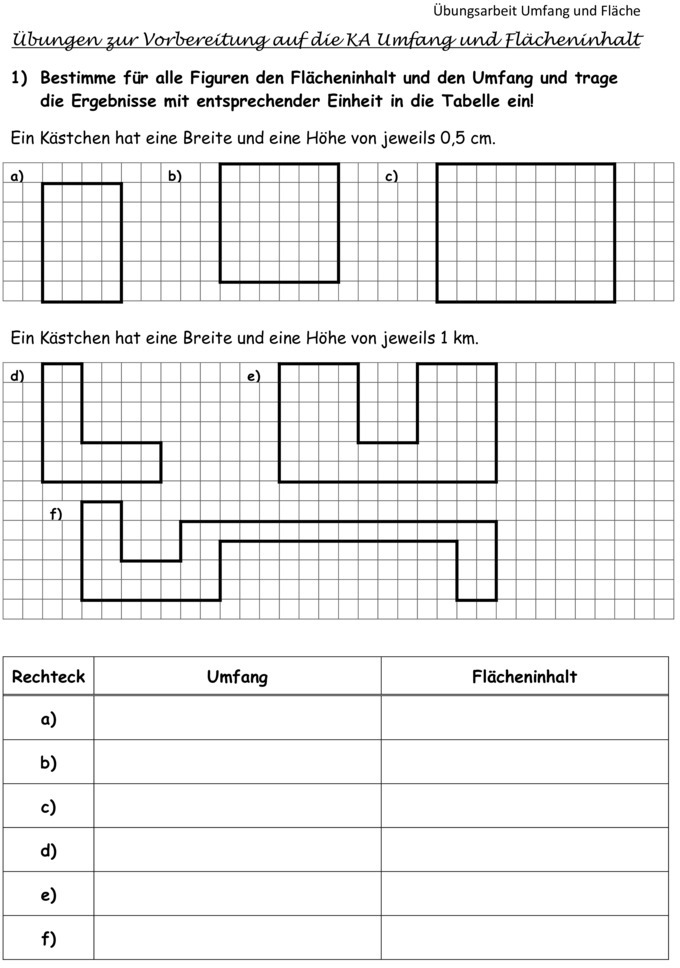
Klassenarbeit zu Umfang Volumen und Flächenberechnung

Hier erfährst du, wie du den Umfang und den Flächeninhalt eines Parallelogramms oder einer Raute berechnen kannst. Höhe von Parallelogramm und Raute. Umfang von Quadrat und Rechteck. Umfang eines Parallelogramms. Umfang einer Raute. Flächeninhalt von Quadrat und Rechteck. Flächeninhalt eines Parallelogramms. Flächeninhalt einer Raute.

Pin auf Brot

Um den Umfang eines Rechtecks oder eines Quadrats zu ermitteln, zählst du einfach alle Seiten zusammen: Quadrat: 12 + 12 + 12 + 12 = 48 12 + 12 + 12 + 12 = 48. Rechteck: 9 + 16 + 9 + 16 = 50 9 + 16 + 9 + 16 = 50. Oder genauer mit den Maßeinheiten: Quadrat: 12 cm + 12 cm + 12 cm + 12 cm = 48 cm 12 c m + 12 c m + 12 c m + 12 c m = 48 c m.

Flächeninhalt Und Umfang Arbeitsblatt

Kreisberechnung - Radius, Durchmesser, Umfang und Kreisfläche. Thema Kreis ﹣ Rechner. Erstellt und aktualisiert von Michael Mühl. Hier dreht sich alles um den Kreis: Definitionen, Formeln und Berechnungen für den Radius, den Durchmesser, den Kreisumfang und die Kreisfläche mit unterschiedlichen Größeneinheiten.

Wunderbar Umfang Und Flächeninhalt Berechnen Bild Ideen und Bilder

Du berechnest den Flächeninhalt zusammengesetzter Figuren, indem du die Figur in berechenbare Figuren zerlegst und die Ergebnisse der Teilflächen addierst. Zur Erinnerung: Flächeninhalt Quadrat: A = a2 A = a 2. Flächeninhalt Rechteck: A = a ⋅ b A = a ⋅ b. Flächeninhalt Dreieck: AD = a ⋅ ha 2 A D = a ⋅ h a 2. Weiter mit dem Umfang.

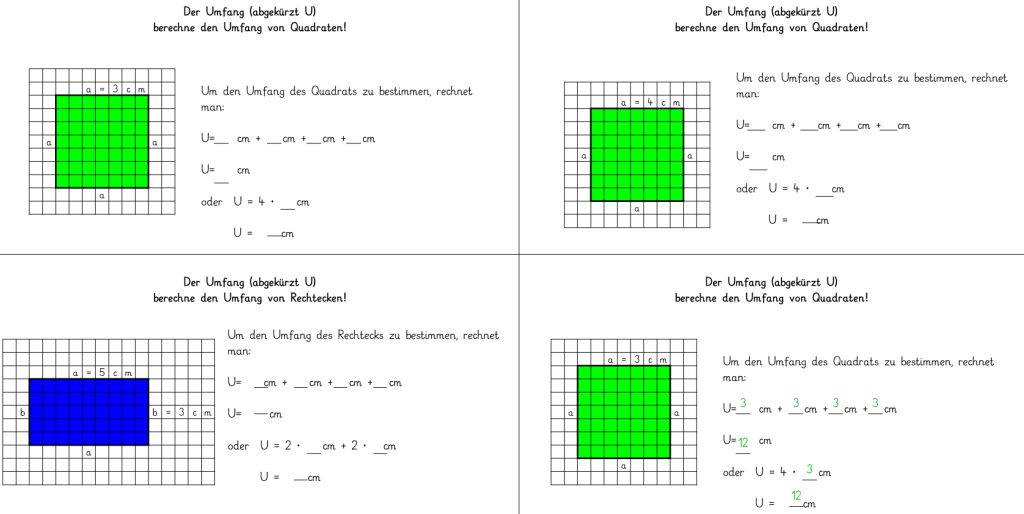
Interaktiv Umfang von Quadrat und Rechteck berechnen • gpaed.de

Formel: A = a · b. "A" ist die Fläche des Rechtecks. "a" ist die Länge der ersten Grundseite. "b" ist die Länge der zweiten Grundseite. Beispiel: a = 5 cm, b = 3 cm. Lösung: A = 5 cm · 3 cm = 15 cm 2. Umfang Rechteck: Formel: U = 2 · a + 2 · b. "U" ist der Umfang des Rechtecks. "a" ist die Länge der ersten Grundseite.

Rechteck Umfang und Flächeninhalt Formel für den Umfang Formel für den Flächeninhalt

Formeln: Umfang: U = 2 ⋅ a + 2 ⋅ b. Flächeninhalt: A = a ⋅ b. Diagonale: d = a 2 + b 2. Mathe einfach erklärt! Unsere Lernhefte für die 5. bis 10. Klasse.