Moment of Inertia of Circular Disk kamaldheeriya YouTube

Moment of Inertia of a Disk plus YouTube

I parallel-axis = 1 2 m d R 2 + m d ( L + R) 2. Adding the moment of inertia of the rod plus the moment of inertia of the disk with a shifted axis of rotation, we find the moment of inertia for the compound object to be. Itotal = 1 3mrL2 + 1 2mdR2 + md(L + R)2. I total = 1 3 m r L 2 + 1 2 m d R 2 + m d ( L + R) 2.

Rotationl dynamic lecture_12./Moment of inertia of a disc YouTube

Moment of Inertia of a Disk. The moment of inertia, which is also denoted by the letter "i", measures the extent to which resistance of an object is rotational acceleration about a particular axis, and is the rotational analog to mass. \ [ML^2\] (mass×length2) is the unit of the dimension of Mass moments of inertia.

JEE Main 2018 Moment of Inertia of Disc With Circular Hole 123IITJEE

I = ∑ I = ∑ mr2. For an extended body, replace the summation with an integral and the mass with an infinitesimal mass. You add up (integrate) all the moments of inertia contributed by the teeny, tiny masses ( dm) located at whatever distance ( r) from the axis they happen to lie. I =. ⌠.

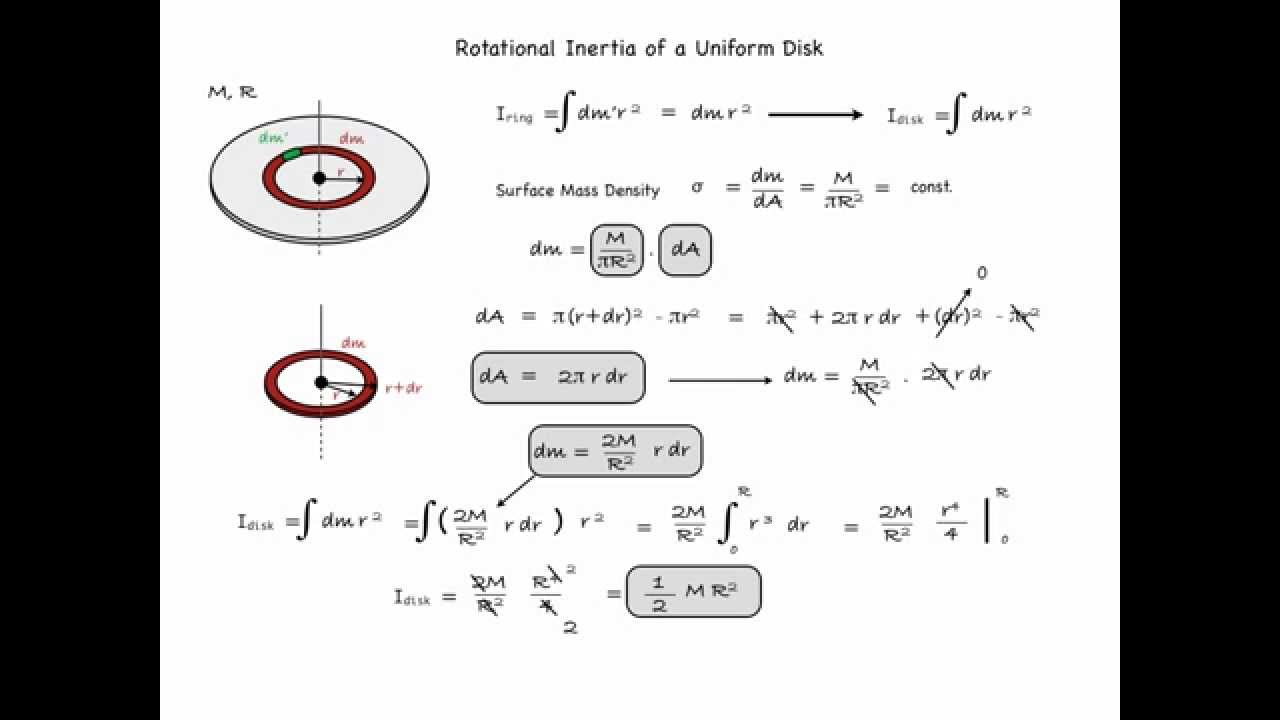
NOVA Physics Rotational Inertia of a Uniform Disk YouTube

For a single particle rotating around a fixed axis, this is straightforward to calculate. We can relate the angular velocity to the magnitude of the translational velocity using the relation vt = ωr v t = ω r, where r is the distance of the particle from the axis of rotation and vt v t is its tangential speed.

How to derive the moment of inertia of a disk YouTube

Theoretically, the rotational inertia, I, of a ring about its center of mass is given by: 2 2 = --M R + R ( 1 2 where M is the mass of the ring, R1 is the inner radius of the ring, and R2 is the outer radius of the ring. See Figure 11.1. The rotational inertia of a disk about its center of mass is given by: I = - 1 -MR2 2

MOMENT OF INERTIA OF A CIRCULAR DISC WITH RESPECT TO IT'S DIAMETER

Axis through center, in plane of plate. Thin Rod. Axis through mid point. Thin Rod. Axis at one end. Moment of Inertia - Rotational inertia for uniform objects with various geometrical shapes.

How to derive the formula for the moment of inertia of a disc about an

The moment of inertia, otherwise known as the mass moment of inertia, angular mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis, akin to how mass determines the force needed for a desired acceleration.

PPT Chapter 10 Rotational motion and Energy PowerPoint Presentation

Rotational inertia is a property of any object which can be rotated. It is a scalar value which tells us how difficult it is to change the rotational velocity of the object around a given rotational axis. Rotational inertia plays a similar role in rotational mechanics to mass in linear mechanics.

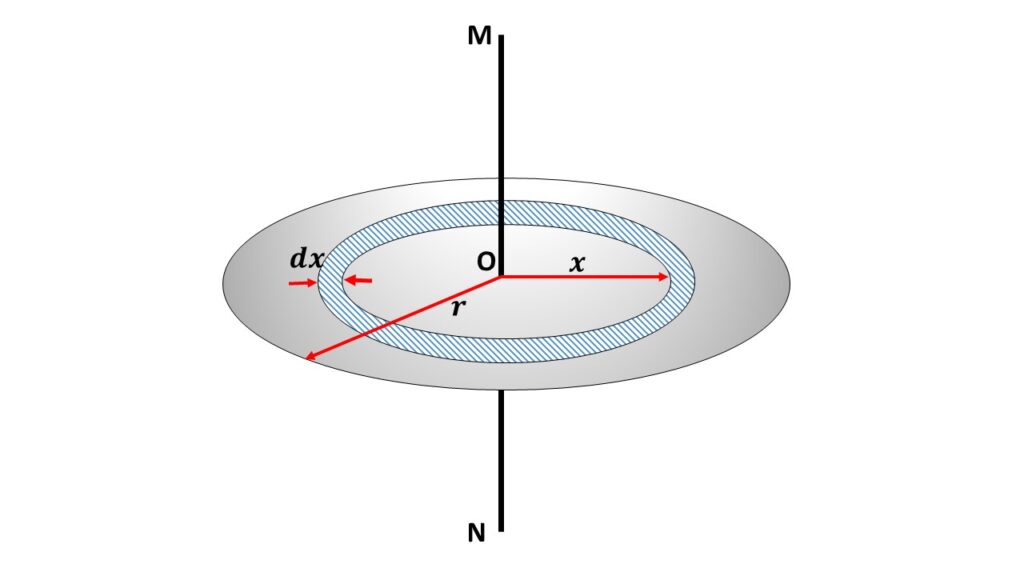
Determine The Moment Of Inertia Of A Plane Circular Disc (i) About An

Moment of inertia, denoted by I, measures the extent to which an object resists rotational acceleration about a particular axis, it is the rotational analogue to mass (which determines an object's resistance to linear acceleration ). The moments of inertia of a mass have units of dimension ML 2 ( [mass] × [length] 2 ).

Moment of Inertia of DISC Rotational Motion Class 11 NEET JEE

III. Measuring the Rotational Inertia of the Metal Disk. In this last activity you will measure the rotational inertia of the metal disk. Remove the metal rod from the encoder, flip the 3-step pulley over, and attach the metal disk to the 3-step pulley. Attach 20 g to the end of the string, press Collect, and release the hanging mass. Record.

Moment of Inertia of a Disk with a Hole YouTube

To develop the precise relationship among force, mass, radius, and angular acceleration, consider what happens if we exert a force F F on a point mass m m that is at a distance r r from a pivot point, as shown in Figure 10.10. Because the force is perpendicular to r r, an acceleration a = F m a = F m is obtained in the direction of F F.

ExampleInertia of disc with point masses YouTube

This last equation is the rotational analog of Newton's second law (F=ma), where torque is analogous to force, angular acceleration is analogous to translational acceleration, and mr 2 is analogous to mass (or inertia).The quantity mr 2 is called the rotational inertia or moment of inertia of a point mass m a distance r from the center of rotation.. Figure 2.

Find the moment of inertia of a circular disk or solid cylinder of

τ = mr2α. (10.3.3) (10.3.3) τ = m r 2 α. This last equation is the rotational analog of Newton's second law F = ma F = m a, where torque is analogous to force, angular acceleration is analogous to translational acceleration, and mr2 m r 2 is analogous to mass (or inertia). The quantity mr2 m r 2 is called the rotational inertia or moment.

Simple trick to understand Moment of Inertia of a Thin Disk. JEE

Considering the rotational part of the system (taking a disk as an example) and ignoring the frictional torque from the axle, we have the following equation from Newton's second law of motion. τ=rT = I. disk. α, (1) where . I. is the moment of inertia of the disk, r. is the radius of the multi-step pulley on the rotary motion sensor and . T

Rotational Mechanics Solved Example 10 Moment of Inertia for Semi

Thus, the rotational inertia of a thin disk about an axis through its CM is the product of one-half the total mass of the disk and the square of its radius. Notice that the thickness of the disk does not effect its rotational inertia. A consequence of this fact is that a cyclinder has the same rotational inertia as a disk, when rotated about an.

Moment of inertia of disk AnswerData

Use Equation 16.3.1 but with the limits changed to x′ = 0 and x′ = L, where x′ = x + L / 2, A disk with mass M and radius R is spinning with angular speed ω about an axis that passes through the rim of the disk perpendicular to its plane. The moment of inertia about cm is Icm = (1 / 2)mR2.